In classical physics, momentum is a simple product of mass and velocity. However, we saw in the last section that when special relativity is taken into account, massive objects have a speed limit. What effect do you think mass and velocity have on the momentum of objects moving at relativistic speeds?

Momentum is one of the most important concepts in physics. The broadest form of Newton’s second law is stated in terms of momentum. Momentum is conserved whenever the net external force on a system is zero. This makes momentum conservation a fundamental tool for analyzing collisions. All of Chapter 7 Work, Energy, and Energy Resources is devoted to momentum, and momentum has been important for many other topics as well, particularly where collisions were involved. We will see that momentum has the same importance in modern physics. Relativistic momentum is conserved, and much of what we know about subatomic structure comes from the analysis of collisions of accelerator-produced relativistic particles.

The first postulate of relativity states that the laws of physics are the same in all inertial frames. Does the law of conservation of momentum survive this requirement at high velocities? The answer is yes, provided that the momentum is defined as follows.

Note that we use [latex]{u}[/latex] for velocity here to distinguish it from relative velocity [latex]{v}[/latex] between observers. Only one observer is being considered here. With [latex]{p}[/latex] defined in this way, total momentum [latex]{p_{\text{tot}}}[/latex] is conserved whenever the net external force is zero, just as in classical physics. Again we see that the relativistic quantity becomes virtually the same as the classical at low velocities. That is, relativistic momentum [latex]{\gamma mu}[/latex] becomes the classical [latex]{mu}[/latex] at low velocities, because [latex]{\gamma}[/latex] is very nearly equal to 1 at low velocities.

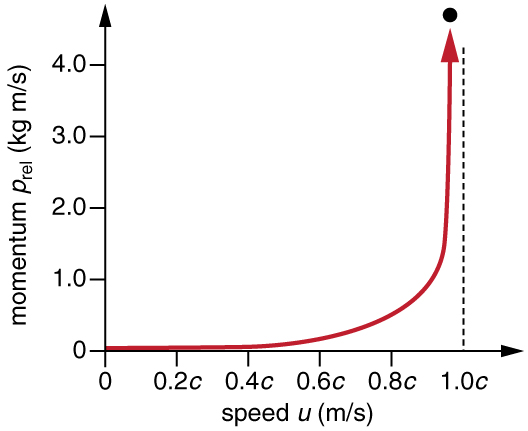
Relativistic momentum has the same intuitive feel as classical momentum. It is greatest for large masses moving at high velocities, but, because of the factor [latex]{\gamma}[/latex], relativistic momentum approaches infinity as[/latex]latex{u}[/latex] approaches [latex]{c}[/latex]. (See Figure 2.) This is another indication that an object with mass cannot reach the speed of light. If it did, its momentum would become infinite, an unreasonable value.

Relativistic momentum is defined in such a way that the conservation of momentum will hold in all inertial frames. Whenever the net external force on a system is zero, relativistic momentum is conserved, just as is the case for classical momentum. This has been verified in numerous experiments.

In Chapter 28.6 Relativistic Energy, the relationship of relativistic momentum to energy is explored. That subject will produce our first inkling that objects without mass may also have momentum.