Chapter 34 Frontiers of Physics

34.6 High-temperature Superconductors

Summary

  • Identify superconductors and their uses.
  • Discuss the need for a high-Tc superconductor.

Superconductors are materials with a resistivity of zero. They are familiar to the general public because of their practical applications and have been mentioned at a number of points in the text. Because the resistance of a piece of superconductor is zero, there are no heat losses for currents through them; they are used in magnets needing high currents, such as in MRI machines, and could cut energy losses in power transmission. But most superconductors must be cooled to temperatures only a few kelvin above absolute zero, a costly procedure limiting their practical applications. In the past decade, tremendous advances have been made in producing materials that become superconductors at relatively high temperatures. There is hope that room temperature superconductors may someday be manufactured.

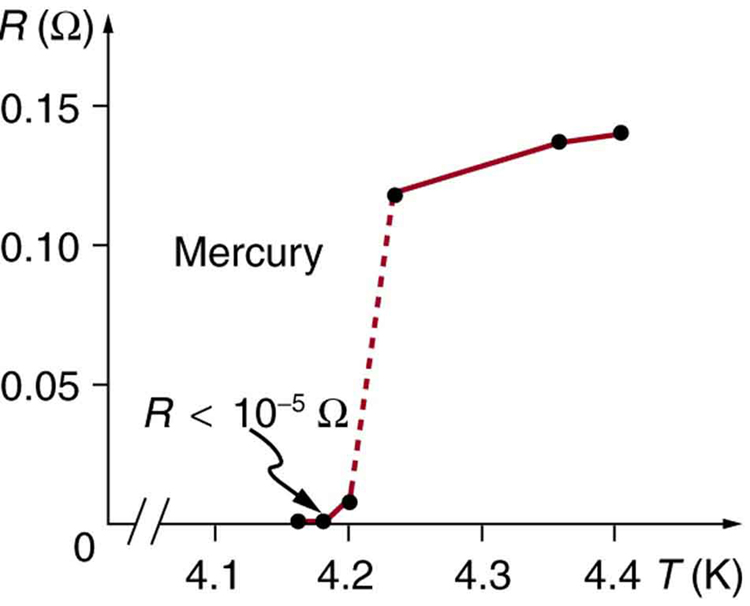
Superconductivity was discovered accidentally in 1911 by the Dutch physicist H. Kamerlingh Onnes (1853–1926) when he used liquid helium to cool mercury. Onnes had been the first person to liquefy helium a few years earlier and was surprised to observe the resistivity of a mediocre conductor like mercury drop to zero at a temperature of 4.2 K. We define the temperature at which and below which a material becomes a superconductor to be its critical temperature, denoted by [latex]{T_c}[/latex]. (See Figure 1.) Progress in understanding how and why a material became a superconductor was relatively slow, with the first workable theory coming in 1957. Certain other elements were also found to become superconductors, but all had [latex]{T_c}[/latex] s less than 10 K, which are expensive to maintain. Although Onnes received a Nobel prize in 1913, it was primarily for his work with liquid helium.

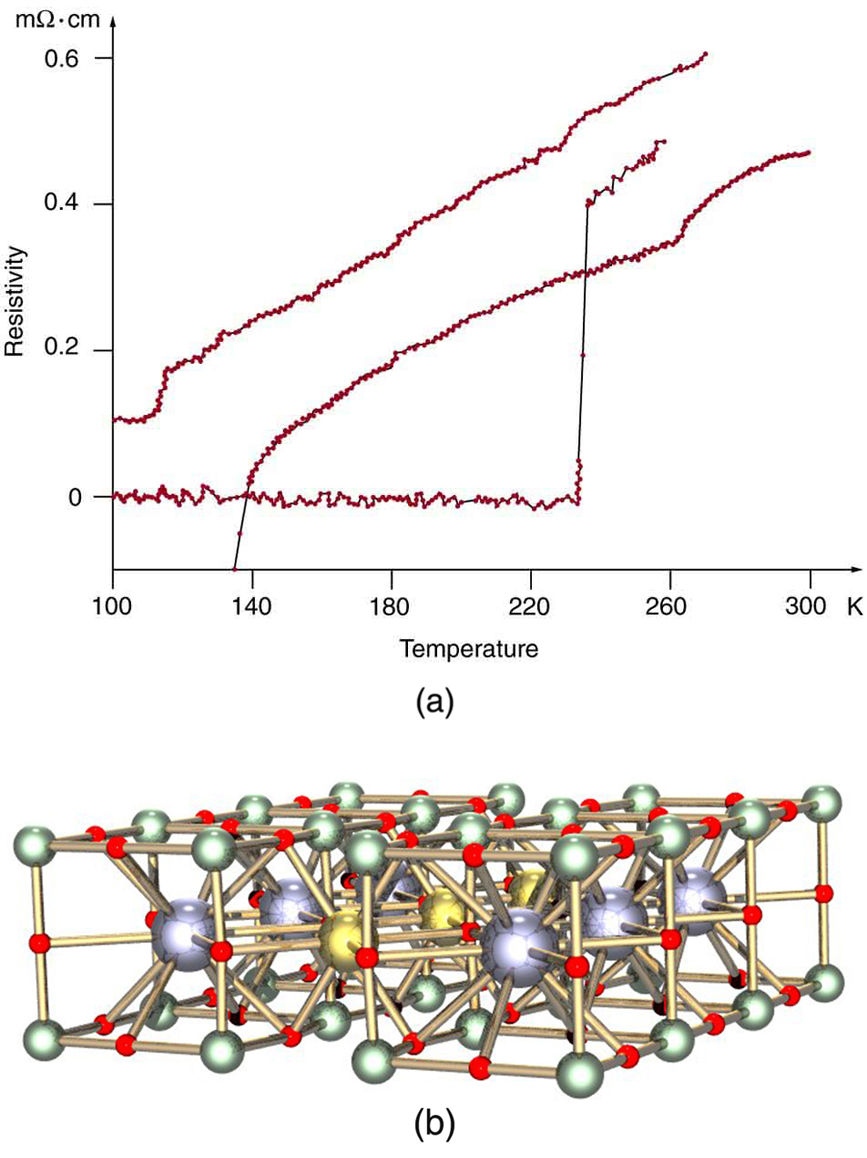
In 1986, a breakthrough was announced—a ceramic compound was found to have an unprecedented [latex]{T_c}[/latex] of 35 K. It looked as if much higher critical temperatures could be possible, and by early 1988 another ceramic (this of thallium, calcium, barium, copper, and oxygen) had been found to have [latex]{T_c = 125 \;\text{K}}[/latex] (see Figure 2.) The economic potential of perfect conductors saving electric energy is immense for [latex]{T_c}[/latex] s above 77 K, since that is the temperature of liquid nitrogen. Although liquid helium has a boiling point of 4 K and can be used to make materials superconducting, it costs about $5 per liter. Liquid nitrogen boils at 77 K, but only costs about $0.30 per liter. There was general euphoria at the discovery of these complex ceramic superconductors, but this soon subsided with the sobering difficulty of forming them into usable wires. The first commercial use of a high temperature superconductor is in an electronic filter for cellular phones. High-temperature superconductors are used in experimental apparatus, and they are actively being researched, particularly in thin film applications.

The graph shows resistivity on the vertical axis and temperature on the horizontal axis. The resistivity goes from zero to zero point one five ohms and the temperature goes from four point one to four point four kelvin. The curve starts at less than ten to the minus five ohms just below four point two kelvin, then jumps up at four point two kelvin to about zero point one two ohms. As the temperature increases further, the resistivity climbs more or less linearly until it reaches about zero point one four ohms at a temperature just above four point four kelvin.
Figure 1. A graph of resistivity versus temperature for a superconductor shows a sharp transition to zero at the critical temperature Tc. High temperature superconductors have verifiable Tc s greater than 125 K, well above the easily achieved 77-K temperature of liquid nitrogen.
The figure shows a button-shaped magnet floating above a superconducting puck. Some wispy fog is flowing from the puck.
Figure 2. One characteristic of a superconductor is that it excludes magnetic flux and, thus, repels other magnets. The small magnet levitated above a high-temperature superconductor, which is cooled by liquid nitrogen, gives evidence that the material is superconducting. When the material warms and becomes conducting, magnetic flux can penetrate it, and the magnet will rest upon it. (credit: Saperaud)

The search is on for even higher [latex]{T_c}[/latex] superconductors, many of complex and exotic copper oxide ceramics, sometimes including strontium, mercury, or yttrium as well as barium, calcium, and other elements. Room temperature (about 293 K) would be ideal, but any temperature close to room temperature is relatively cheap to produce and maintain. There are persistent reports of [latex]{T_c}[/latex] s over 200 K and some in the vicinity of 270 K. Unfortunately, these observations are not routinely reproducible, with samples losing their superconducting nature once heated and recooled (cycled) a few times (see Figure 3.) They are now called USOs or unidentified superconducting objects, out of frustration and the refusal of some samples to show high [latex]{T_c}[/latex] even though produced in the same manner as others. Reproducibility is crucial to discovery, and researchers are justifiably reluctant to claim the breakthrough they all seek. Time will tell whether USOs are real or an experimental quirk.

The theory of ordinary superconductors is difficult, involving quantum effects for widely separated electrons traveling through a material. Electrons couple in a manner that allows them to get through the material without losing energy to it, making it a superconductor. High- [latex]{T_c}[/latex] superconductors are more difficult to understand theoretically, but theorists seem to be closing in on a workable theory. The difficulty of understanding how electrons can sneak through materials without losing energy in collisions is even greater at higher temperatures, where vibrating atoms should get in the way. Discoverers of high [latex]{T_c}[/latex] may feel something analogous to what a politician once said upon an unexpected election victory—“I wonder what we did right?”

Figure a is a graph of resistivity versus temperature. The resistivity goes from zero to zero point six milli ohm centimeters and the temperature goes from one hundred to three hundred kelvin. There are three curves on the graph. The first curve starts near zero point one milli ohm centimeters, one hundred kelvin, and increases linearly to zero point six milli ohm centimeters, two hundred and eighty kelvin. The second curve is at zero resistivity from 100 kelvin to about two hundred and thirty five kelvin, then jumps straight up to zero point four milli ohm centimeters, after which it increases linearly with temperature with the same slope as the first curve. The third curve has one point at minus zero point zero five milli ohm centimeters at about one hundred and thirty kelvin, then becomes positive and increases essentially linearly with the same slope as the first curve. Figure b shows a scaffolding structure made up of rods. At each vertex in the scaffold there is a ball that is either white, red, purple, or blue. Each color represents a different kind of atom. The white balls are the largest, then the red, then the purple, and the blue balls are the smallest. The balls are arranged in a systematic pattern. From bottom to top the scaffold layers are formed from white and red balls, then red and blue balls, then purple balls, then again red and blue balls, then finally white and red balls again. In each individual layer the balls form various grid patterns. This scaffold structure forms a brick-like shape and an identical such brick is positioned above it with a gap between the two bricks. The two bricks are connected together by a single layer of blue balls.
Figure 3. (a) This graph, adapted from an article in Physics Today, shows the behavior of a single sample of a high-temperature superconductor in three different trials. In one case the sample exhibited a Tc of about 230 K, whereas in the others it did not become superconducting at all. The lack of reproducibility is typical of forefront experiments and prohibits definitive conclusions. (b) This colorful diagram shows the complex but systematic nature of the lattice structure of a high-temperature superconducting ceramic. (credit: en:Cadmium, Wikimedia Commons)

Section Summary

  • High-temperature superconductors are materials that become superconducting at temperatures well above a few kelvin.
  • The critical temperature [latex]{T_c}[/latex] is the temperature below which a material is superconducting.
  • Some high-temperature superconductors have verified [latex]{T_c}[/latex] s above 125 K, and there are reports of [latex]{T_c}[/latex] s as high as 250 K.

Conceptual Questions

1: What is critical temperature [latex]{T_c}[/latex]? Do all materials have a critical temperature? Explain why or why not.

2: Explain how good thermal contact with liquid nitrogen can keep objects at a temperature of 77 K (liquid nitrogen’s boiling point at atmospheric pressure).

3: Not only is liquid nitrogen a cheaper coolant than liquid helium, its boiling point is higher (77 K vs. 4.2 K). How does higher temperature help lower the cost of cooling a material? Explain in terms of the rate of heat transfer being related to the temperature difference between the sample and its surroundings.

Problems & Exercises

1: A section of superconducting wire carries a current of 100 A and requires 1.00 L of liquid nitrogen per hour to keep it below its critical temperature. For it to be economically advantageous to use a superconducting wire, the cost of cooling the wire must be less than the cost of energy lost to heat in the wire. Assume that the cost of liquid nitrogen is $0.30 per liter, and that electric energy costs $0.10 per kW·h. What is the resistance of a normal wire that costs as much in wasted electric energy as the cost of liquid nitrogen for the superconductor?

Glossary

Superconductors
materials with resistivity of zero
critical temperature
the temperature at which and below which a material becomes a superconductor

Solutions

Problems & Exercises

1: [latex]{0.30 \;\Omega}[/latex]

 

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book