21.6 DC Circuits Containing Resistors and Capacitors

Paul Peter Urone; Roger Hinrichs

Chapter 21 Circuits and DC Instruments

21.6 DC Circuits Containing Resistors and Capacitors

Summary

Explain the importance of the time constant, $τ$ , and calculate the time constant for a given resistance and capacitance.
Explain why batteries in a flashlight gradually lose power and the light dims over time.
Describe what happens to a graph of the voltage across a capacitor over time as it charges.
Explain how a timing circuit works and list some applications.
Calculate the necessary speed of a strobe flash needed to “stop” the movement of an object over a particular length.

When you use a flash camera, it takes a few seconds to charge the capacitor that powers the flash. The light flash discharges the capacitor in a tiny fraction of a second. Why does charging take longer than discharging? This question and a number of other phenomena that involve charging and discharging capacitors are discussed in this module.

RC Circuits

An $R C$ circuit is one containing a resistor $R$ and a capacitor $C$ . The capacitor is an electrical component that stores electric charge.

Figure 1 shows a simple $R C$ circuit that employs a DC (direct current) voltage source. The capacitor is initially uncharged. As soon as the switch is closed, current flows to and from the initially uncharged capacitor. As charge increases on the capacitor plates, there is increasing opposition to the flow of charge by the repulsion of like charges on each plate.

In terms of voltage, this is because voltage across the capacitor is given by $V_{c} = Q / C$ , where $Q$ is the amount of charge stored on each plate and $C$ is the capacitance. This voltage opposes the battery, growing from zero to the maximum emf when fully charged. The current thus decreases from its initial value of $I_{0} = \frac{emf}{R}$ to zero as the voltage on the capacitor reaches the same value as the emf. When there is no current, there is no $I R$ drop, and so the voltage on the capacitor must then equal the emf of the voltage source. This can also be explained with Kirchhoff’s second rule (the loop rule), discussed in Chapter 21.3 Kirchhoff’s Rules, which says that the algebraic sum of changes in potential around any closed loop must be zero.

The initial current is $I_{0} = \frac{emf}{R}$ , because all of the $I R$ drop is in the resistance. Therefore, the smaller the resistance, the faster a given capacitor will be charged. Note that the internal resistance of the voltage source is included in $R$ , as are the resistances of the capacitor and the connecting wires. In the flash camera scenario above, when the batteries powering the camera begin to wear out, their internal resistance rises, reducing the current and lengthening the time it takes to get ready for the next flash.

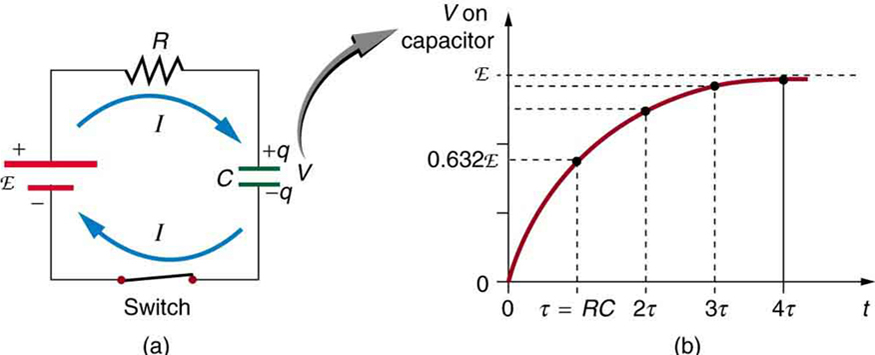
Part a shows a circuit with a cell of e m f script E connected in series with a resistor R, a capacitor C, and a switch to close the circuit. The current is shown flowing in a clockwise direction. The capacitor plates are shown to have a charge positive q and negative q respectively. Part b shows a graph of the variation of voltage of the capacitor with time. The voltage is plotted along the vertical axis and the time is along the horizontal axis. The graph shows a smooth upward rising curve which approaches a maximum and flattens out at maximum voltage equal to e m f script E over time. — **Figure 1.** (a) An RC circuit with an initially uncharged capacitor. Current flows in the direction shown (opposite of electron flow) as soon as the switch is closed. Mutual repulsion of like charges in the capacitor progressively slows the flow as the capacitor is charged, stopping the current when the capacitor is fully charged and Q = C ⋅ emf. (b) A graph of voltage across the capacitor versus time, with the switch closing at time t = 0. (Note that in the two parts of the figure, the capital script E stands for emf, q stands for the charge stored on the capacitor, and τ is the RC time constant.)

Voltage on the capacitor is initially zero and rises rapidly at first, since the initial current is a maximum. Figure 1(b) shows a graph of capacitor voltage versus time ( $t$ ) starting when the switch is closed at $t = 0$ . The voltage approaches emf asymptotically, since the closer it gets to emf the less current flows. The equation for voltage versus time when charging a capacitor $C$ through a resistor $R$ , derived using calculus, is

V = emf (1 - e^{- t / R C}) (charging),

where $V$ is the voltage across the capacitor, emf is equal to the emf of the DC voltage source, and the exponential e = 2.718 … is the base of the natural logarithm. Note that the units of $R C$ are seconds. We define

τ = RC,

where $τ$ (the Greek letter tau) is called the time constant for an $R C$ circuit. As noted before, a small resistance $R$ allows the capacitor to charge faster. This is reasonable, since a larger current flows through a smaller resistance. It is also reasonable that the smaller the capacitor $C$ , the less time needed to charge it. Both factors are contained in $τ = R C$ .

More quantitatively, consider what happens when $t = τ = R C$ . Then the voltage on the capacitor is

V = emf (1 - e^{- 1}) = emf (1 - 0.368) = 0.632 \cdot emf .

This means that in the time $τ = R C$ , the voltage rises to 0.632 of its final value. The voltage will rise 0.632 of the remainder in the next time $τ$ . It is a characteristic of the exponential function that the final value is never reached, but 0.632 of the remainder to that value is achieved in every time, $τ$ . In just a few multiples of the time constant $τ$ , then, the final value is very nearly achieved, as the graph in Figure 1(b) illustrates.

Discharging a Capacitor

Discharging a capacitor through a resistor proceeds in a similar fashion, as Figure 2 illustrates. Initially, the current is $I_{0} = \frac{V_{0}}{R}$ , driven by the initial voltage $V_{0}$ on the capacitor. As the voltage decreases, the current and hence the rate of discharge decreases, implying another exponential formula for $V$ . Using calculus, the voltage $V$ on a capacitor $C$ being discharged through a resistor $R$ is found to be

V = V_{0} e^{- t / R C} (discharging) .

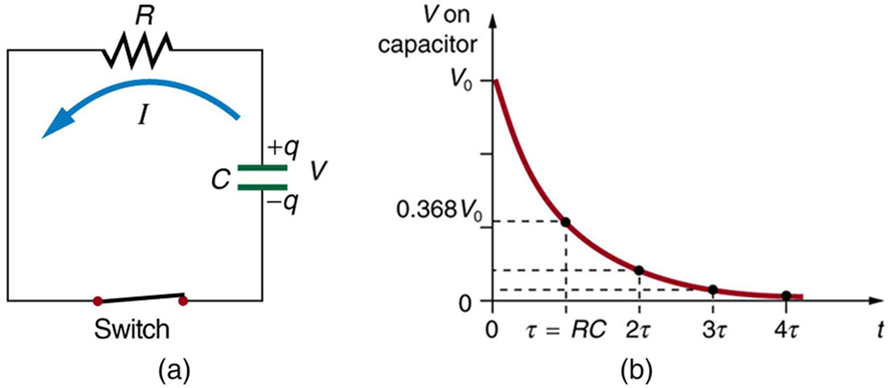
Part a shows a circuit with a capacitor C connected in series with a resistor R and a switch to close the circuit. The current is shown flowing in a counterclockwise direction. The capacitor plates are shown to have a charge positive q and negative q respectively. Part b shows a graph of the variation of voltage across the capacitor with time. The voltage is plotted along the vertical axis and the time is along the horizontal axis. The graph shows a smooth downward falling curve which approaches a minimum and flattens out close to zero over time. — **Figure 2.** (a) Closing the switch discharges the capacitor C through the resistor R. Mutual repulsion of like charges on each plate drives the current. (b) A graph of voltage across the capacitor versus time, with *V = V*₀ at t = 0. The voltage decreases exponentially, falling a fixed fraction of the way to zero in each subsequent time constant τ.

The graph in Figure 2(b) is an example of this exponential decay. Again, the time constant is $τ = R C$ . A small resistance $R$ allows the capacitor to discharge in a small time, since the current is larger. Similarly, a small capacitance requires less time to discharge, since less charge is stored. In the first time interval $τ = R C$ after the switch is closed, the voltage falls to 0.368 of its initial value, since $V = V_{0} \cdot e^{- 1} = 0.368 V_{0}$ .

During each successive time $τ$ , the voltage falls to 0.368 of its preceding value. In a few multiples of $τ$ , the voltage becomes very close to zero, as indicated by the graph in Figure 2(b).

Now we can explain why the flash camera in our scenario takes so much longer to charge than discharge; the resistance while charging is significantly greater than while discharging. The internal resistance of the battery accounts for most of the resistance while charging. As the battery ages, the increasing internal resistance makes the charging process even slower. (You may have noticed this.)

The flash discharge is through a low-resistance ionized gas in the flash tube and proceeds very rapidly. Flash photographs, such as in Figure 3, can capture a brief instant of a rapid motion because the flash can be less than a microsecond in duration. Such flashes can be made extremely intense.

During World War II, nighttime reconnaissance photographs were made from the air with a single flash illuminating more than a square kilometer of enemy territory. The brevity of the flash eliminated blurring due to the surveillance aircraft’s motion. Today, an important use of intense flash lamps is to pump energy into a laser. The short intense flash can rapidly energize a laser and allow it to reemit the energy in another form.

In the photograph, details of the fast beating wings of the hummingbird taking nectar from a flower have been caught in focus, instead of the blur that our eyes would see in real time. — **Figure 3.** This stop-motion photograph of a rufous hummingbird (*Selasphorus rufus*) feeding on a flower was obtained with an extremely brief and intense flash of light powered by the discharge of a capacitor through a gas. (credit: Dean E. Biggins, U.S. Fish and Wildlife Service)

Integrated Concept Problem: Calculating Capacitor Size—Strobe Lights

High-speed flash photography was pioneered by Doc Edgerton in the 1930s, while he was a professor of electrical engineering at MIT. You might have seen examples of his work in the amazing shots of hummingbirds in motion, a drop of milk splattering on a table, or a bullet penetrating an apple (see Figure 3). To stop the motion and capture these pictures, one needs a high-intensity, very short pulsed flash, as mentioned earlier in this module.

Suppose one wished to capture the picture of a bullet (moving at $5.0 \times 10^{2} m / s$ ) that was passing through an apple. The duration of the flash is related to the $R C$ time constant, $τ$ . What size capacitor would one need in the $R C$ circuit to succeed, if the resistance of the flash tube was $10.0 Ω$ ? Assume the apple is a sphere with a diameter of $8.0 \times 10^{- 2} m$ .

Strategy

We begin by identifying the physical principles involved. This example deals with the strobe light, as discussed above. Figure 2 shows the circuit for this probe. The characteristic time $τ$ of the strobe is given as $τ = R C$ .

Solution

We wish to find $C$ , but we don’t know $τ$ . We want the flash to be on only while the bullet traverses the apple. So we need to use the kinematic equations that describe the relationship between distance $x$ , velocity $v$ , and time $t$ :

x = v t or t =

\frac{x}{v} .

The bullet’s velocity is given as $5.0 \times 10^{2} m / s$ , and the distance $x$ is $8.0 \times 10^{- 2} m$ . The traverse time, then, is

t =

\frac{x}{v}

=

\frac{8.0 \times 10^{- 2} m}{5.0 \times 10^{2} m / s}

= 1.6 \times 10^{- 4} s

.

We set this value for the crossing time $t$ equal to $τ$ . Therefore,

C =

\frac{t}{R}

=

\frac{1.6 \times 10^{- 4} s}{10.0 Ω}

= 16 μ F

.

(Note: Capacitance $C$ is typically measured in farads, $F$ , defined as Coulombs per volt. From the equation, we see that $C$ can also be stated in units of seconds per ohm.)

Discussion

The flash interval of $160 μ s$ (the traverse time of the bullet) is relatively easy to obtain today. Strobe lights have opened up new worlds from science to entertainment. The information from the picture of the apple and bullet was used in the Warren Commission Report on the assassination of President John F. Kennedy in 1963 to confirm that only one bullet was fired.

RC Circuits for Timing

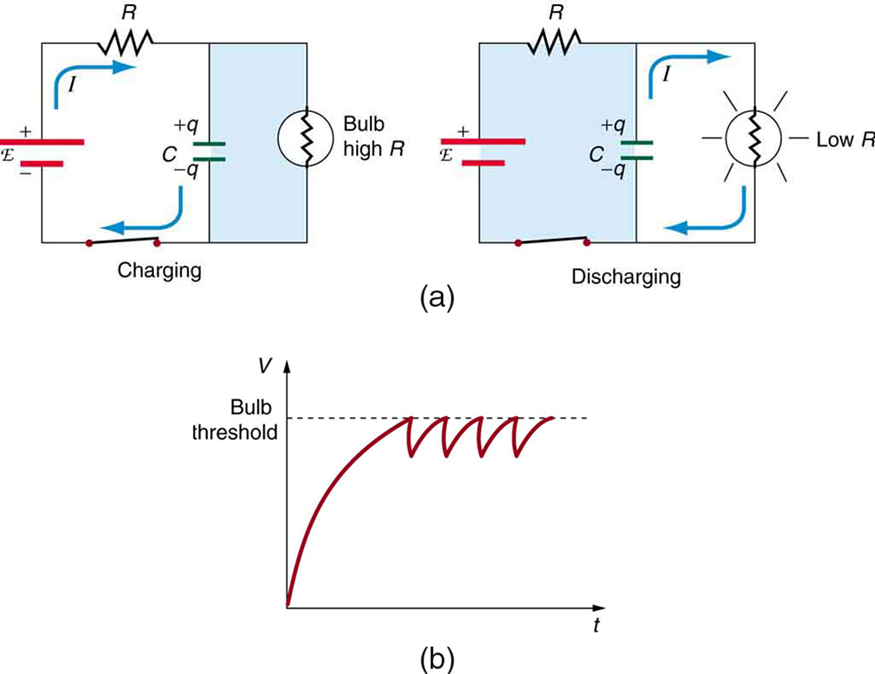
$R C$ circuits are commonly used for timing purposes. A mundane example of this is found in the ubiquitous intermittent wiper systems of modern cars. The time between wipes is varied by adjusting the resistance in an $R C$ circuit. Another example of an $R C$ circuit is found in novelty jewelry, Halloween costumes, and various toys that have battery-powered flashing lights. (See Figure 4 for a timing circuit.)

A more crucial use of $R C$ circuits for timing purposes is in the artificial pacemaker, used to control heart rate. The heart rate is normally controlled by electrical signals generated by the sino-atrial (SA) node, which is on the wall of the right atrium chamber. This causes the muscles to contract and pump blood. Sometimes the heart rhythm is abnormal and the heartbeat is too high or too low.

The artificial pacemaker is inserted near the heart to provide electrical signals to the heart when needed with the appropriate time constant. Pacemakers have sensors that detect body motion and breathing to increase the heart rate during exercise to meet the body’s increased needs for blood and oxygen.

Part a shows a charging circuit containing cell of e m f script E connected to a resistor R and capacitor C and a closed switch to complete the circuit. The current is shown to flow clockwise through this arm of the circuit alone. A bulb of high resistance R is connected across the capacitor. Part b shows a discharging circuit containing a cell of e m f script E connected to a resistor R and capacitor C and a closed switch to complete the circuit. A bulb of low resistance R is connected across the capacitor. Current flows clockwise through the arm containing the capacitor and the low resistance bulb. Part c is a graph showing variation of voltage verses time for the bulb in above circuit. The voltage is plotted along the vertical axis and the time is plotted along the horizontal axis. The curve has a smooth rise from the origin, reaches a plateau at threshold value of voltage where it begins to drop and rise as a small sawtooth wave with maxima lying along the threshold line. — **Figure 4.** (a) The lamp in this RC circuit ordinarily has a very high resistance, so that the battery charges the capacitor as if the lamp were not there. When the voltage reaches a threshold value, a current flows through the lamp that dramatically reduces its resistance, and the capacitor discharges through the lamp as if the battery and charging resistor were not there. Once discharged, the process starts again, with the flash period determined by the RC constant τ. (b) A graph of voltage versus time for this circuit.

Calculating Time: RC Circuit in a Heart Defibrillator

A heart defibrillator is used to resuscitate an accident victim by discharging a capacitor through the trunk of her body. A simplified version of the circuit is seen in Figure 2. (a) What is the time constant if an $8.00 - μ F$ capacitor is used and the path resistance through her body is $1.00 \times 10^{3} Ω$ ? (b) If the initial voltage is 10.0 kV, how long does it take to decline to $5.00 \times 10^{2} V$ ?

Strategy

Since the resistance and capacitance are given, it is straightforward to multiply them to give the time constant asked for in part (a). To find the time for the voltage to decline to $5.00 \times 10^{2} V$ , we repeatedly multiply the initial voltage by 0.368 until a voltage less than or equal to $5.00 \times 10^{2} V$ is obtained. Each multiplication corresponds to a time of $τ$ seconds.

Solution for (a)

The time constant $τ$ is given by the equation $τ = R C$ . Entering the given values for resistance and capacitance (and remembering that units for a farad can be expressed as $s / Ω$ ) gives

τ = R C = (1.00 \times 10^{3} Ω) (8.00 μ F) = 8.00 ms .

Solution for (b)

In the first 8.00 ms, the voltage (10.0 kV) declines to 0.368 of its initial value. That is:

V = 0.368 V_{0} = 3.680 \times 10^{3} V at t = 8.00 ms .

(Notice that we carry an extra digit for each intermediate calculation.) After another 8.00 ms, we multiply by 0.368 again, and the voltage is

\begin{aligned} V^{'} = & 0.368 V \\ = & (0.368) (3.680 \times 10^{3} V) \\ = & 1.354 \times 10^{3} V at t = 16.0 ms . \end{aligned}

Similarly, after another 8.00 ms, the voltage is

\begin{aligned} V^{'}^{'} = & 0.368 V^{'} = (0.368) (1.354 \times 10^{3} V) \\ = & 498 V at t = 24.0 ms . \end{aligned}

Discussion

So after only 24.0 ms, the voltage is down to 498 V, or 4.98% of its original value. Such brief times are useful in heart defibrillation, because the brief but intense current causes a brief but effective contraction of the heart. The actual circuit in a heart defibrillator is slightly more complex than the one in Figure 2, to compensate for magnetic and AC effects that will be covered in Chapter 22 Magnetism.

Check Your Understanding

1: When is the potential difference across a capacitor an emf?

PhET Explorations: Circuit Construction Kit (DC only)

An electronics kit in your computer! Build circuits with resistors, light bulbs, batteries, and switches. Take measurements with the realistic ammeter and voltmeter. View the circuit as a schematic diagram, or switch to a life-like view.

Section Summary

An $R C$ circuit is one that has both a resistor and a capacitor.
The time constant $τ$ for an $R C$ circuit is $τ = R C$ .
When an initially uncharged ( $V_{0} = 0$ at $t = 0$ ) capacitor in series with a resistor is charged by a DC voltage source, the voltage rises, asymptotically approaching the emf of the voltage source; as a function of time,
$V = emf (1 - e^{- t / R C}) (charging) .$
Within the span of each time constant $τ$ , the voltage rises by 0.632 of the remaining value, approaching the final voltage asymptotically.
If a capacitor with an initial voltage $V_{0}$ is discharged through a resistor starting at $t = 0$ , then its voltage decreases exponentially as given by
$V = V_{0} e^{- t / R C} (discharging) .$
In each time constant $τ$ , the voltage falls by 0.368 of its remaining initial value, approaching zero asymptotically.

Conceptual Questions

1: Regarding the units involved in the relationship $τ = R C$ , verify that the units of resistance times capacitance are time, that is, $Ω \cdot F = s$ .

2: The $R C$ time constant in heart defibrillation is crucial to limiting the time the current flows. If the capacitance in the defibrillation unit is fixed, how would you manipulate resistance in the circuit to adjust the $R C$ constant $τ$ ? Would an adjustment of the applied voltage also be needed to ensure that the current delivered has an appropriate value?

3: When making an ECG measurement, it is important to measure voltage variations over small time intervals. The time is limited by the $R C$ constant of the circuit—it is not possible to measure time variations shorter than $R C$ . How would you manipulate $R$ and $C$ in the circuit to allow the necessary measurements?

4: Draw two graphs of charge versus time on a capacitor. Draw one for charging an initially uncharged capacitor in series with a resistor, as in the circuit in Figure 1, starting from $t = 0$ . Draw the other for discharging a capacitor through a resistor, as in the circuit in Figure 2, starting at $t = 0$ , with an initial charge $Q_{0}$ . Show at least two intervals of $τ$ .

5: When charging a capacitor, as discussed in conjunction with Figure 1, how long does it take for the voltage on the capacitor to reach emf? Is this a problem?

6: When discharging a capacitor, as discussed in conjunction with Figure 2, how long does it take for the voltage on the capacitor to reach zero? Is this a problem?

7: Referring to Figure 1, draw a graph of potential difference across the resistor versus time, showing at least two intervals of $τ$ . Also draw a graph of current versus time for this situation.

8: A long, inexpensive extension cord is connected from inside the house to a refrigerator outside. The refrigerator doesn’t run as it should. What might be the problem?

9: In Figure 4, does the graph indicate the time constant is shorter for discharging than for charging? Would you expect ionized gas to have low resistance? How would you adjust $R$ to get a longer time between flashes? Would adjusting $R$ affect the discharge time?

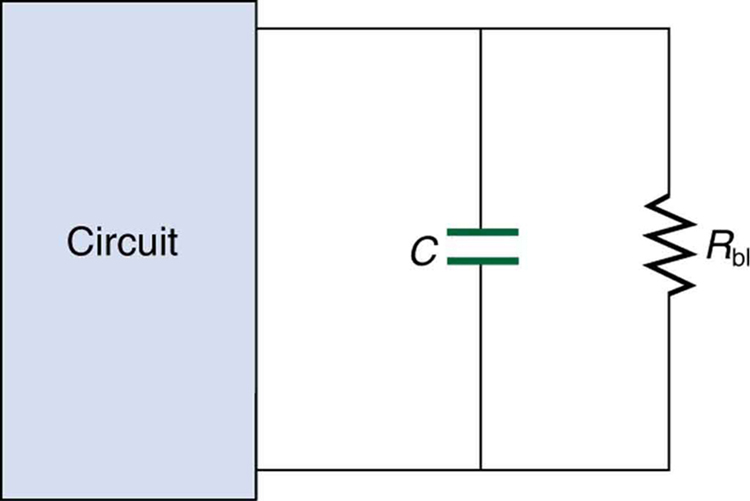
10: An electronic apparatus may have large capacitors at high voltage in the power supply section, presenting a shock hazard even when the apparatus is switched off. A “bleeder resistor” is therefore placed across such a capacitor, as shown schematically in Figure 6, to bleed the charge from it after the apparatus is off. Why must the bleeder resistance be much greater than the effective resistance of the rest of the circuit? How does this affect the time constant for discharging the capacitor?

An electrical circuit with a capacitor has an extra resistor R sub b l, called a bleeder, installed in parallel with the capacitor. — **Figure 6.** A bleeder resistor R_bl discharges the capacitor in this electronic device once it is switched off.

Problem Exercises

1: The timing device in an automobile’s intermittent wiper system is based on an $R C$ time constant and utilizes a $0.500 - μ F$ capacitor and a variable resistor. Over what range must $R$ be made to vary to achieve time constants from 2.00 to 15.0 s?

2: A heart pacemaker fires 72 times a minute, each time a 25.0-nF capacitor is charged (by a battery in series with a resistor) to 0.632 of its full voltage. What is the value of the resistance?

3: The duration of a photographic flash is related to an $R C$ time constant, which is $0.100 μ s$ for a certain camera. (a) If the resistance of the flash lamp is $0.0400 Ω$ during discharge, what is the size of the capacitor supplying its energy? (b) What is the time constant for charging the capacitor, if the charging resistance is $800 k Ω$ ?

4: A 2.00- and a $7.50 - μ F$ capacitor can be connected in series or parallel, as can a 25.0- and a $100 - k Ω$ resistor. Calculate the four $R C$ time constants possible from connecting the resulting capacitance and resistance in series.

5: After two time constants, what percentage of the final voltage, emf, is on an initially uncharged capacitor $C$ , charged through a resistance $R$ ?

6: A $500 - Ω$ resistor, an uncharged $1.50 - μ F$ capacitor, and a 6.16-V emf are connected in series. (a) What is the initial current? (b) What is the $R C$ time constant? (c) What is the current after one time constant? (d) What is the voltage on the capacitor after one time constant?

7: A heart defibrillator being used on a patient has an $R C$ time constant of 10.0 ms due to the resistance of the patient and the capacitance of the defibrillator. (a) If the defibrillator has an $8.00 - μ F$ capacitance, what is the resistance of the path through the patient? (You may neglect the capacitance of the patient and the resistance of the defibrillator.) (b) If the initial voltage is 12.0 kV, how long does it take to decline to $6.00 \times 10^{2} V$ ?

8: An ECG monitor must have an $R C$ time constant less than $1.00 \times 10^{2} μ s$ to be able to measure variations in voltage over small time intervals. (a) If the resistance of the circuit (due mostly to that of the patient’s chest) is $1.00 k Ω$ , what is the maximum capacitance of the circuit? (b) Would it be difficult in practice to limit the capacitance to less than the value found in (a)?

9: Figure 7 shows how a bleeder resistor is used to discharge a capacitor after an electronic device is shut off, allowing a person to work on the electronics with less risk of shock. (a) What is the time constant? (b) How long will it take to reduce the voltage on the capacitor to 0.250% (5% of 5%) of its full value once discharge begins? (c) If the capacitor is charged to a voltage $V_{0}$ through a $100 - Ω$ resistance, calculate the time it takes to rise to $0.865 V$ (This is about two time constants.)

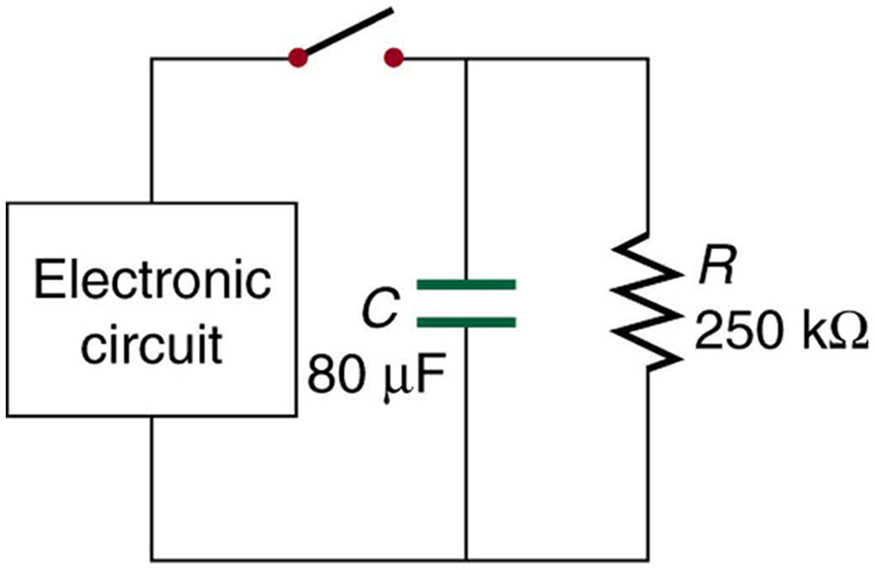
A parallel circuit with a switch, an embedded electronic circuit, a capacitor, and a resistor is shown. The embedded circuit, capacitor, and resistor are connected in parallel with each other: the electronic circuit on the left, the capacitor in the middle, and the resistor on the right. The capacitor has a capacitance of eighty micro farads. The resistor has a resistance of two hundred fifty kilohms. The switch is on the top, between the electronic circuit and the capacitor leg. — **Figure 7.**

10: Using the exact exponential treatment, find how much time is required to discharge a $250 - μ F$ capacitor through a $500 - Ω$ resistor down to 1.00% of its original voltage.

11: Using the exact exponential treatment, find how much time is required to charge an initially uncharged 100-pF capacitor through a $75.0 - M Ω$ resistor to 90.0% of its final voltage.

12: Integrated Concepts

If you wish to take a picture of a bullet traveling at 500 m/s, then a very brief flash of light produced by an $R C$ discharge through a flash tube can limit blurring. Assuming 1.00 mm of motion during one $R C$ constant is acceptable, and given that the flash is driven by a $600 - μ F$ capacitor, what is the resistance in the flash tube?

13: Integrated Concepts

A flashing lamp in a Christmas earring is based on an $R C$ discharge of a capacitor through its resistance. The effective duration of the flash is 0.250 s, during which it produces an average 0.500 W from an average 3.00 V. (a) What energy does it dissipate? (b) How much charge moves through the lamp? (c) Find the capacitance. (d) What is the resistance of the lamp?

14: Integrated Concepts

A $160 - μ F$ capacitor charged to 450 V is discharged through a $31.2 - k Ω$ resistor. (a) Find the time constant. (b) Calculate the temperature increase of the resistor, given that its mass is 2.50 g and its specific heat is $1.67 \frac{kJ}{kg \cdot^{\circ} C}$ , noting that most of the thermal energy is retained in the short time of the discharge. (c) Calculate the new resistance, assuming it is pure carbon. (d) Does this change in resistance seem significant?

16: Unreasonable Results

(a) Calculate the capacitance needed to get an $R C$ time constant of $1.00 \times 10^{3} s$ with a $0.100 - Ω$ resistor. (b) What is unreasonable about this result? (c) Which assumptions are responsible?

17: Construct Your Own Problem

Consider a camera’s flash unit. Construct a problem in which you calculate the size of the capacitor that stores energy for the flash lamp. Among the things to be considered are the voltage applied to the capacitor, the energy needed in the flash and the associated charge needed on the capacitor, the resistance of the flash lamp during discharge, and the desired $R C$ time constant.

18: Construct Your Own Problem

Consider a rechargeable lithium cell that is to be used to power a camcorder. Construct a problem in which you calculate the internal resistance of the cell during normal operation. Also, calculate the minimum voltage output of a battery charger to be used to recharge your lithium cell. Among the things to be considered are the emf and useful terminal voltage of a lithium cell and the current it should be able to supply to a camcorder.

Glossary

RC circuit: a circuit that contains both a resistor and a capacitor

capacitor: an electrical component used to store energy by separating electric charge on two opposing plates

capacitance: the maximum amount of electric potential energy that can be stored (or separated) for a given electric potential

Solutions

Check Your Understanding

1: Only when the current being drawn from or put into the capacitor is zero. Capacitors, like batteries, have internal resistance, so their output voltage is not an emf unless current is zero. This is difficult to measure in practice so we refer to a capacitor’s voltage rather than its emf. But the source of potential difference in a capacitor is fundamental and it is an emf.

Problem Exercises

1: $range 4.00 to 30.0 M Ω$

3: (a) $2.50 μ F$

(b) 2.00 s

5: 86.5%

7: (a) $1.25 k Ω$

(b) 30.0 ms

9: (a) 20.0 s

(b) 120 s

(c) 16.0 ms

11: $1.73 \times 10^{- 2} s$

12: $3.33 \times 10^{- 3} Ω$

15: (a) 4.99 s

(b) $3.87^{\circ} C$

(c) $31.1 k Ω$

(d) No

License

Icon for the Creative Commons Attribution 4.0 International License