What does the observer see?

We look at the physical world around us, like this image of a football game, hoping our team wins the game. You gaze at the stars on a clear night in the mountains, letting their beauty answer your soul. You wait to catch a wave at the beach, trying to get down the timing of the waves and judge the height of each wave so that you can body surf all the way back to shore. You listen to the sound of a steak sizzling on the barbecue grill, and you smell for the smell of a “done” steak, so that you can prepare to gustate joyfully with your family at the table. From each observation, we hope to draw out a message: the beauty of the stars, the excellence of a wave, the doneness of a steak. A scientist might observe so that she can discern the geometric structure of the DNA molecule,

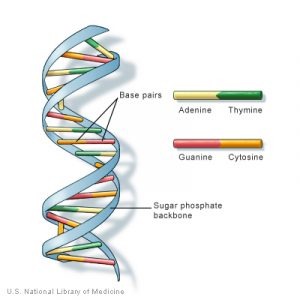
so that he can connect the magnetic field to an electrical current, so that the scientist can explain all the laws of Nature in a satisfying manner, a single, simple view of everything. It begins with that which the observer sees.

Our book’s cover photograph shows a mayhem of football players in the mud and rain. What message can we draw out of it? The players must be trying to advance the football in a given direction, but where is the football? In which direction is the ball actually moving? Is this the direction the football coach intends the ball to advance? Each player in the photograph is doing something to another player, moving in three dimensions. Is the player executing the “X’s and O’s” for his part of the offensive play, or has his interaction with the other players deflected him from the X’s and O’s, from the plan of execution?

The fans in the stands also want to know the future state of play: will their team advance the ball and earn a first down? Will their team score on this play? Will their team win the game? From what they see, they try to predict — part of the fun of going to a game.

Another prominent observer is the referee. Are the players following the rules or infracting the rules? Has the ball crossed the goal line? The referee says, “I call ‘em like I see ‘em!” That is, he makes decisions based on observation.

A sports writer observes the mayhem closely, perhaps making notes, so that he can render a report about what happened on the field and why.

Mutatis mutandam, the scientist observes his world and attempts to answer questions about the things he sees. Is there a plan or pattern in what he sees? Is there a clear interaction of the physical objects that he observes? What will be the future state of the things he sees? How can he present his findings so that another scientist can comprehend it?

Predicting what comes next

The most easily understood scientific task is simply to predict the future state of an object: where will that object be in a few moments’ time. Where do the electrons go? Will the baseball clear the outfield fence, winning the game, or will the centerfielder race underneath it and make a miracle catch on the warning track? Where does the spacecraft go on its way to Mars?

The matter of spacecraft heading for Mars is not a facetious idea: it is a significant prediction, a prediction that must be solid and on the mark, because, in the recent past, NASA has lost spacecraft. In 1999, the Mars Climate Orbiter did disappear when it was attempting to synch up with Mars and start its orbit around the red planet. The NASA navigation team’s prediction that it would safely hit the optimal altitude, 226 kilometers above the surface of Mars, was grossly incorrect. The spacecraft disappeared. No one knows whether it crashed on Mars or skipped back out into space, never to return. NASA’s later backtracking calculations showed that the spacecraft attempted to insert itself into orbit at an altitude of just 57 kilometers^[1], an error of 169 kilometers, which error is approximately the distance between Orlando and Tampa. That is a big error, a bad miss.
So, yes, we scientists want to be able to predict position and velocity and as many other quantities as possible.

The School of Galileo

Whether calculating a prediction or working out some other problem, we students of science are students in the school of Galileo. He founded this school in Italy, almost 400 years ago in the Renaissance. In a written disputation about comets, he wrote two pointed sentences about philosophy — his word for physical science — two sentences about science that were new and controversial in his day and which we still follow in our day:

The universe is not random; it has a comprehensible language, but what is the nature of that language?  Its essential language is not social. That is, we do not judge the truth of a scientific statement based on how many Facebook friends the statement might have.
Science does not have a musical language, though that would be a lively, fun science if it were musical.

Professor Galileo was convinced that the language of Nature was geometric and mathematical, and that our comprehension of Nature must therefore include mathematical structures. So as we follow Galileo’s lead, we will seek explanations of the universe we see around us, expecting that those explanations have a mathematical backbone.

N.b. In this specific course of study, PSC1121 Physical Science in the Florida K-20 system, expect to use a small amount of mathematics, including proportions, simple equations, but no logarithms, no trigonometry other than Pythagorean Theorem, and no calculus. No worries! Mathematics professor Galileo did not know any calculus, either. The world had to wait until Sir Isaac Newton got around to inventing calculus, and Newton was born in 1642, the year of Galileo’s death. Yet even without explicit calculus and without the bulk of trigonometry, we will still attain a good grip on the character of physical laws.