Main Body
Chapter 2, States of Motion: Galileo’s Breakthrough
brueckner
Galileo contra Aristotle
-Aristotle, Physics, Book II
—Galilei, Galileo, Dialogue Concerning the Two Chief World Systems. Translated by Stillman Drake, California: University of California Press, 1632.
It is safe to say that Aristotle, renowned and influential for many centuries, definitely got on Galileo’s nerves when it came to physics.
This is also true concerning the lazy-thinking followers of Aristotle in Galileo’s day. Galileo made sure that, in his classes, conclusions based on observations, particularly observations of measurable quantities, had the power to lock down a physical concept. No amount of philosophical hot air could defeat a set of measurements from the great book of nature. Authority resides not in the famous books of Aristotle but in the great book of nature, of which one makes observation and takes measurement.
Galileo simplified his task by sticking to measurable motions.
Aristotle’s book, Physics, concerned motion, but he also included a diversity of motions that we and our professor, Galileo, would not include in a physics text. For instance, under the topic of motion, Aristotle considered this question, “Why did the Spartans go to war?” That is a motion of a kind, but not measurable with meter sticks and a pendulum. Aristotle also considered the change of bronze into a bronze statue. He considered aging, learning, doctoring, rolling, building and leaping as motions. A projectile, like an arrow shot from a bow, is propelled along its path by the air behind it through which it has already moved, according to Aristotle. To read Aristotle on this topic is to learn patience — it is very complicated.
Galileo simplified his task. He restricted his study of motion to positions and distances, times and intervals of time, from Event A in space and time, to event B in space and time, events between which a time interval and a distance interval could be calculated. In a previous chapter, we considered a short history of events on the Florida Turnpike, viz.
| Event | Position | Time |
| A | Mile marker 259 | 1:55:08 PM, 9/31/15 |
| B | Mile marker 266.8 | 3:55:08 PM, 9/31/15 |
The distance interval is 7.8 miles, 13 km. The time interval is two hours, 7200 seconds. From these kinds of measurements, Galileo has something to say. For instance, he might say that the driver’s average speed is 3.9 mph.
However, from this short table of information, neither we nor Galileo can derive any accelerations of the car along the turnpike.
What is the difference between an accelerated state of motion and one without acceleration?
Galileo took a freely falling body as his exemplar of accelerated motion. One could study all other types of accelerated motion using free-fall acceleration concepts.
When, therefore, I observe a stone initially at rest falling from an elevated position and continually acquiring new increments of speed, why should I not believe that such increases take place in a manner which is exceedingly simple and rather obvious to everybody? If now we examine the matter carefully we find no addition or increment more simple than that which repeats itself always in the same manner.”
– Galileo, Dialogues Concerning Two New Sciences, Day 3[1]
Of critical importance is the idea of “continually acquiring new increments of speed… which repeats itself always in the same manner.” This is what we mean about the acceleration of an object in free fall, that for every second of free fall in the gravitational field at the surface of Earth, the downward speed increases 9.8 m/sec, always in the same manner, until it impacts the ground. We customarily call this acceleration g,
![]()
This is the acceleration everyone on Earth feels every day. Astronauts up in the International Space Station, ISS, of course, feel a bit less acceleration, being a significant distance up in space above the surface of Earth. For everyone on Earth, though, from the top of Mount Everest to the deeps of the Mariana Trench in the Pacific Ocean, g is our gravitational acceleration, courtesy of all the kilograms of Earth’s mass.
Is there a state in between accelerated states?
Galileo’s first conclusion concerning free fall and vertical acceleration was that two inclined planes of equal heights but different tilt angles would still accelerate a ball to the same speed at the bottom of the ramp. For instance, two inclined planes of height 0.10 m, i.e., 10 cm, and bases 1.0 m and 0.5 m, have tilt angles 5.7º and 11.3º respectively.
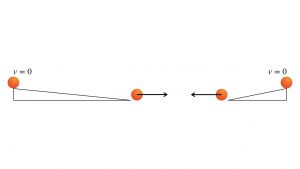
If released from rest at the top of the ramp, each ball acquires the same speed. In this diagram, the length of the arrows is the same, indicating equal speeds. The acceleration of gravity, g, is responsible for accelerating each ball to its later speed, even though it is not straight down free fall.
Given an inclined plane of any angle, you can figure out the fraction of g that pulls an object down the slope.
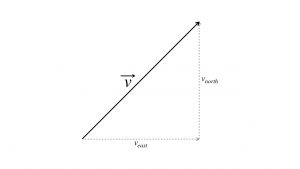
Just as a bird flying northeast has some speed directly to the north and some speed perpendicular to that, to the east, so an object on a ramp, with tilt angle ![]() ,
,
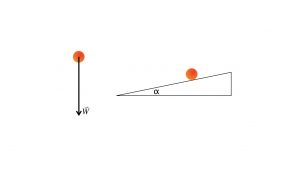
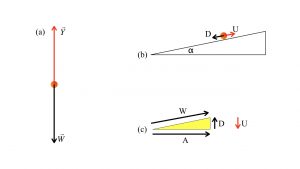
will get a fraction of g down the ramp and a fraction of g perpendicular to that, into the ramp. To figure out the proportions, rotate the inclined plane triangle so that the inclined surface becomes horizontal, as in Fig. 2a. Then sketch out an accelerations triangle of the same shape, like the yellow triangle in Fig. 2a. Now flip it and rotate the yellow triangle so that its short side is along the ramp surface, as shown in Fig. 2b. Figure 2c shows the “exploded” version of the yellow accelerations triangle, with the longest side labeled g, the downslope fraction labeled D, and the fraction absorbed by the ramp labeled A. Galileo showed that this similar triangle gives you the fraction of g that accelerates a body down the inclined plane. The fraction into the ramp has no affect, if the ramp is rigid. But the fraction of g along the downslope gets the object moving.
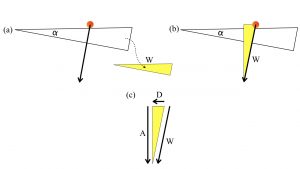
Another way to interpret this result, using proportional triangles, is to say that the amount of gravitational pull down the ramp, D, is the same size pull, U, that you need to exert up the ramp, to keep the object at rest. Your pull U balances gravity’s pull D.
Galileo used inclined plane results like this to attack other problems. Eventually, he tackled the problem of a projectile moving through its arc. He proved that, ignoring the air resistance, the path of a projectile through the air is a parabola. He envisioned a horizontal plane along which an object moves at a constant speed, that the horizontal plane came to the end, and that the object keeps moving out past the edge of the plane, like a Ferrari driving off a cliff. His analysis of the object’s motion rested on two assumptions:
- that the motion retained its horizontal component unperturbed, and
- that the object acquired equal increments of downward speed in equal intervals of time, in the normal free fall manner.
Aristotle would never have accepted this splitting of the motion into independently analyzable parts, horizontal and vertical, nor would he have accepted that a state of motion could persist, unperturbed, at constant speed. Aristotle knew only a state of rest and a state of forced motion, a moveable object moved by a mover. Galileo insisted on this.
Galileo insisted on unperturbed motion horizontally at constant speed, adding a third state to the roster of possible states of motion.
Galileo’s roster of states of motion
- accelerated motion due to a force like gravity,
- a state of rest,
- a state of motion at constant speed, in a constant direction,
He asserted this with confidence because he had experimented with his inclined planes. He knew that, on a horizontal plane, an object would be indifferent to being at rest or to moving along a horizontal line at constant speed.
How Galileo taught the third state of motion
Galileo taught this idea to his students at Pisa in the following manner. Consider for a moment that you were comparing motions of an object on an ideal, frictionless inclined plane to its motion on an ideal, frictionless horizontal plane.
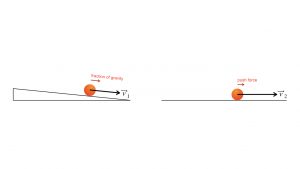
The object on the ramp gets a small fraction of the full free fall force of gravity, as usual. In addition, you maintain, contra Professor Galileo, that the object on the horizontal plane needs a certain minimum amount of OOMPH to get it going along the plane, denoted by the small red push force vector. We will call that amount of push ![]() . According to you, the object will move along the horizontal plane only if it experiences this amount of push. Your push force
. According to you, the object will move along the horizontal plane only if it experiences this amount of push. Your push force ![]() might be 0.02 metric units of force.
might be 0.02 metric units of force.
At this point, Aristotle would be smiling at you, saying, “Οε τρίγωνο αγόρι! Είναι τα γενέθλιά σας!”[2]
In addition, say that the object’s vertical weight force is W; thus, the value of W might be 0.10 metric units of force. To support that object hanging on a string, you need an equally sized force Y, 0.10 metric units of force, pointed upward.
The ratio of the two forces, your conjectured push force on the object and the ordinary weight force of the object, p:W, is 1:5 in this example. That ratio, 1:5, between your conjectured push force and the object’s ordinary weight force, now becomes the key, viz.
Dialogue concerning the third state of motion
Professor Galileo or any of his deputies would now direct you to construct an inclined plane with height 1 unit of length and hypotenuse 5 units in length.
Prof. Galileo: So, you think that spherical object needs 0.02 of your force units to keep it going at a constant speed on my horizontal frictionless plane?
You: Yes, professor, 0.02 metric units of force, tops.
Aristotle: Keep going, kid!
Prof. Galileo: Tell me, youngster, what is the weight of this spherical object?
You: Oh, yes, we balanced it with 0.10 metric units of weight in a balance, so the sphere’s weight is also 0.10 metric units of weight force.
Galileo: Forsooth! You claim that an object whose weight is 0.10 units must get 0.02 units of force on the horizontal, frictionless plane just to keep going at some constant speed.
You: Yes, Prof. Galileo, that is my claim, and I consider it to be true. After all, my other tutor, Dr. Aristotle, makes the same claim, and after all, Aristotle was your teacher, so that is good enough for me, I’d say.
Prof. Galileo: And good enough for government work, no doubt.
You: Yes, that is correct.
Prof. Galileo: So, in general, then, a 1:5 ratio will do the job of keeping an object in motion at constant speed on a frictionless, horizontal plane.
You: Well, professor, I am not sure about “in general,” but for this example, yes, that is the ratio, 1:5, or 20 percent.
Aristotle: Good work, kid, use those high tech terms like “percent” to keep him on his toes!
Prof. Galileo: Yes, my illustrious teacher, it is important to stay on one’s toes so that one’s feet do not get tangled up in the truth and trip one up.
[Laughter]
Prof. Galileo: Now, youngster, take this 1.00 meter board and tilt is up so that its upper end is 20 centimeters above the floor, making a triangle for which the ratio of hypotenuse to height is 1:5. Can you do that?
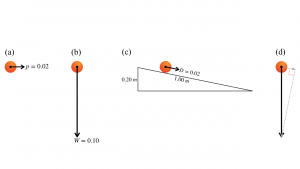
You: Yes, professor. Here we go, yes, that is 20 centimeters up.
Prof. Galileo: now take this steel sphere, which I had designed for this moment — a weight of 0.10 of your metric force units — and roll it down the ramp, just to check its velocity state. [Hands over a steel ball bearing of diameter 5 centimeters]
You: There is goes, down the ramp, acquiring equal increments of speed for each second of motion.
Prof. Galileo: Good eyes, youngster. In other words, it is accelerating down the ramp because of a force that points down the ramp. Do you recall how to calculate the size of that force down the ramp?
Aristotle: Easy does it, kid! You have to apply some trigonometry now.
You: No problema, O mighty teacher, Aristotle! Trigonometry is not too hard here, because it is enough to know the dimensions of the ramp. If the ramp is 1:5, as we constructed, then the downhill force, D, and the total weight force will also be 1:5.
[Crickets]
You: Uh, oh.
Prof. Galileo: Ah! You see my point, now, I presume?
You: Well, look. If the straight down weight force on the ball is 0.10 units, and the ramp ratio is 1:5, then the downhill force on the ball is 0.02 units.
Aristotle: What is wrong with that?
You: Don’t you see? If 0.02 units of force is the force down the ramp, accelerating the ball, how can it also be the size of the force that keeps the same object at constant speed on Professor Galileo’s horizontal, frictionless plane? On the horizontal, frictionless plane it should be smaller than 0.02 units of force.
Aristotle: By Zeus, you have a point, youngster! So maybe the push force is just a little smaller, like 0.01 units of force. That gives you a ratio of 1:10, and 10 is a special number. Add up the first four numbers, ![]() and you get 10, and don’t forget: there are 4 forces in nature in the Standard Model — gravitation, electromagnetic, weak nuclear force and the strong nuclear force — but wait! There are four elements in nature — earth, water, air, and fire, so let’s go with 0.01 units of force.
and you get 10, and don’t forget: there are 4 forces in nature in the Standard Model — gravitation, electromagnetic, weak nuclear force and the strong nuclear force — but wait! There are four elements in nature — earth, water, air, and fire, so let’s go with 0.01 units of force.
Galileo: My dear teacher, Aristotle…
Aristotle: Yes, 0.01 units of force, that’s the ticket.
You: Well, four forces, four elements, four seasons, that’s all very nice, the number ten, so tremendous. But…
Galileo: But… what?
You: Obviously, I could build another ramp with that same board, but 10 centimeters tall, and then we’d be at the same trap: 0.01 units of force down the ramp, so 0.01 units of force cannot be the force that keeps the ball rolling at constant speed along the frictionless, horizontal plane. Has to be smaller than 0.01 units of force.
Galileo: And therefore, my wonderful student…
You: Therefore any positive number for the push for ![]() is too large, and furthermore the only possible value is zero. Which means…
is too large, and furthermore the only possible value is zero. Which means…
Aristotle: Which means I was wrong, kid.
Prof. Galileo: Which means there is a state of motion, constant speed in a constant direction, a state of motion that needs no force to keep it going. On the frictionless, horizontal surface, the object does not care beans about being at rest or at constant velocity.
You: So you were right, Professor Galileo. That third state of motion does exist.
Aristotle: Well, I am convinced. Good work, my wonderful students! Just like in a good kung fu movie, the students have become the master!
This state of motion, at constant speed and constant direction, is in between Aristotle’s two states, rest and forced motion. Perhaps we can give Aristotle his due. He worked hard with what he had. We have also improved our view of the elements of nature: Aristotle numbered four elements, fire, air, water, earth. However, in the past century or so, we have extended and refined the list of elements to over 100 on the periodic table. This concept, the inertial state of motion, is crucial to our entire scientific enterprise, where making predictions and designs requires accurate computation that truly models nature itself.
The parabolic shape of the path of a projectile develops out of the two separated equations of motion,
- of an object in an inertial state of motion going horizontally off the edge of a horizontal plane at speed
 , and
, and - of the same object starting suddenly to drop.
If one starts the clock at the instant the object goes over the side, and if one takes that edge of the plane to be the ![]() origin of the x-y coordinate system, then the positions become functions of time,
origin of the x-y coordinate system, then the positions become functions of time, ![]() and
and ![]() , pronounced “x of t” and “y of t,” viz.
, pronounced “x of t” and “y of t,” viz.
![]()
![]()
Now, rearrange the first equation so that
![]()
We can now put the quotient, ![]() in the y equation wherever
in the y equation wherever ![]() is. Then the formula for y becomes a function of x,
is. Then the formula for y becomes a function of x,
![]()
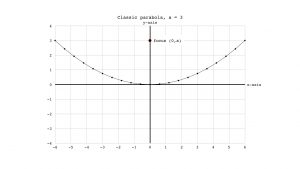
in the classic form that parabolas take, with a factor of x2, just as you might remember it from geometry class in high school.
K
| Classic formula of a parabola on (x,y) graph paper. | Galileo’s parabola in free fall |
|
|
|
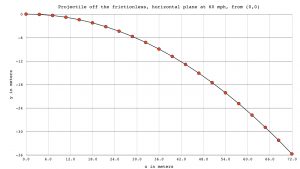
For a projectile, the shape is an up side down parabola, because of free fall. That is, the acceleration of gravity is downward. We should therefore use ![]() in the drop distance formula. Here is a projectile in motion off a frictionless, horizontal plane, with initial speed
in the drop distance formula. Here is a projectile in motion off a frictionless, horizontal plane, with initial speed ![]() , and with the edge of the plane at
, and with the edge of the plane at ![]() . It is an up side down semi-parabola, with impact about 36 m below the plane,
. It is an up side down semi-parabola, with impact about 36 m below the plane, ![]() , and about 72 meters to the right,
, and about 72 meters to the right, ![]()
A full trajectory of a projectile, like a baseball heading for the outfield, would be a full parabola, up side down.
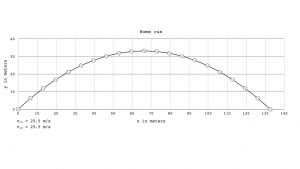
The diagram above is a real “moon shot” home run at Tropicana Field, where the fence in deep center is 404 feet from home plate. or, 123 meters. The initial speed components, ![]() and
and ![]() , are
, are ![]() .
.

“Tropicana Field”by Kwong Yee Cheng is licensed under CC BY-NC-SA 2.0
We have mentioned the downward force of gravity and fractions of it along the surface of an inclined plane. In the next chapter, we will make a systematic survey of the concept of force, as we study Sir Isaac Newton’s three laws of motion.
- Galileo Galilei, Dialogues Concerning Two New Sciences by Galileo Galilei. Translated from the Italian and Latin into English by Henry Crew and Alfonso de Salvio. With an Introduction by Antonio Favaro (New York: Macmillan, 1914). May 5, 2015. http://oll.libertyfund.org/titles/753#Galileo_0416_552 ↵
-  “Go trig boy! It’s your birthday!” ↵


