Interacting skateboarders provide an elementary but powerful picture of all dynamical interactions, from the quantum world of the atom to the celestial world of the great superclusters of galaxies.

How does momentum change the way interactions look?

The key to understanding interaction is momentum, especially in the context of Newton’s third law of action and reaction. As a matter of fact, Newton defined momentum on the very first page of his Principia, in his second definition. He referred to it as the “quantity of motion” that an object has; nowadays we call it the momentum. The momentum formula is

the product of mass in kilograms and speed or velocity in meters per second. One can use the scalar equation in many situations, but momentum is properly a spatial vector and can have components in any of the three spatial dimensions: .

Because Newton’s laws refer to force, mass and acceleration,

and not to momentum, we must do a bit of work to show that his laws do actually involve momentum, though the equations will appear a bit differently. If an object’s mass is constant, like the mass of a cannonball in free-fall from the top of the Tower of Pisa, then then the combination in the previous equation is really the difference of momentum: . So

Impulse, NASA and Hidden Figures

N.b. This result, is not always useful in a complex system, like a rocket launched from Kennedy Space Center.  This is because a rocket motor blasts many kilograms of fuel out the nozzle, generating impulse, but also changing the mass significantly.  Both the mass and the velocity change, so our transformation is not necessarily allowed.  As a result, one needs a bit of calculus to handle momentum and impulse in a system like that.  The famous book and film, “Hidden Figures,” is about the black women who, from WWII and up to the present day, did calculate formulas like that and even more difficult equations.  It is well worth reading that book, seeing that film and reading more, especially about Katherine Johnson, who started out as a math teacher but became such an important scientist in the NASA space program.  Long may she reign!

Now we can see that Newton’s third law tells how to handle interaction, and we can see what will be equal in each interaction, viz.

Here is the list of equal quantities in the third law:

1. The forces are equal. So the first skateboarder pushes on the second with the same number of Newtons as the second skateboarder pushes on the first. With negative meaning opposite direction, .
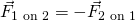2. The amount of time they are in contact, Δt, is of course, the same.
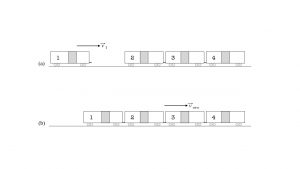
3. Therefore the amount of momentum change 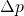is the same, though opposite in direction,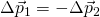

This shows that the equal but opposite reaction is encoded as changes in momentum, Δp. A certain amount of momentum is exchanged between interacting skateboarders.

Momentum is also exchanged between Earth and moon, a certain amount for every second of interaction, and directed in opposite directions. Momentum is exchanged between bat and baseball when the baseball player gets a hit, a certain amount for every millisecond of interaction.

“Baseball”by PMillera4 is licensed under CC BY-NC-ND 2.0

We call that momentum change the impulse imparted to the object, and it depends upon the interaction force, , and the interaction time, .

This equation is known as the impulse equation.

Skateboarders example

Let’s consider two skateboarders in detail, and make some calculations. For our example, let’s look at Carl, whose mass is , and Bob, whose mass is . Carl could be a 5th grader and Bob a high schooler. Let’s also say that they push off from each other, their mutual muscle powers exerting of force on each other, and that they do so for .

There are two ways to analyze the dynamical states of these two skateboarders:

1. If you analyze in terms of forces, you can figure out accelerations for each, then a change of velocity, 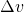, for each.
2. If you focus on momenta, you can calculate a change of momentum, 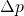, for each.

The change of momentum must be consistent with the results from the analysis by forces.

TWO SKATEBOARDERS Carl’s mass,              Bob’s mass, Initial conditions: both at rest, Bob pushes right, Carl pushes left. Size of interaction force is 500 N. Duration of interaction is 0.48 second. Positive denotes rightward, negative denotes leftward.
Force view	Momentum view
Interaction forces:	Impulses:
Carl’s acceleration:	Carl’s :
Carl’s :	Carl’s momentum states:
Carl’s velocity states:	Bob’s :
Bob’s acceleration:	Bob’s momentum states:
Bob’s :	Check on Carl’s final velocity state: ✔
Bob’s velocity states:	Check on Bob’s final velocity state: ✔

Notice that in the forces view, the accelerations are not equal — Carl gets more acceleration. Also the sizes of are different — again, Carl gets more . So what was Sir Isaac Newton thinking when he said “equal and opposite reaction” in the third law?

He was thinking about momentum! In the momentum view, the skateboarders’ values actually are equal in magnitude, though their vectors have opposite directions, positive for rightward, negative for leftward.

We have now answered the initial question on how momentum changes the look of interaction and “equal but opposite reaction.”

Is there any other pattern in the momentum states of interacting objects?

As a prototype of more complex interaction, the skateboarders also show us how momentum is conserved.  When there are no external forces acting, like a little sister interfering with Carl’s trajectory to the right, the sum of Carl’s and Bob’s momenta, before they interact, is exactly zero. Perhaps that is not very surprising, because they are both at rest. But after 0.48 seconds of interaction, they are moving in different velocity states, but the sum of their final momenta, and , is still zero!

In general the momenta if any number of objects, mutually interacting, have no external forces acting, then their net momentum before interaction is the same as their net momentum afterward. This is the idea of conservation of momentum.

Freight trains give us another everyday example of conservation of momentum. Consider a set of four identical boxcars interacting in a freight yard. Let’s say they each have a mass of 10 metric tons, . Before interaction, (a) one box car has speed , rightward, heading for the other three boxcars, which are at rest.

The single moving car latches onto the set of three, and they move off to the right at some new speed, . The moving boxcar shares its initial momentum with the three other boxcars.  They have latched together (b) and we can treat them as a single moving object of mass .

Before interaction, the total momentum sum, , includes one term from the moving boxcar and one term of zero momentum from the set of three stationary cars, viz.

The total momentum before collision is .

However, after they interact and latch together, the total momentum sum, , contains only one term, for the new set of four boxcars together, total mass.

Since there are no unbalanced external forces in this idealized example, the momentum after must also be , as it was before, i.e.,

Therefore, due to conservation of momentum, we can predict that this set of four boxcars will move off to the right at speed .

With this new information, , the dispatcher in the freight yard can place this string of boxcars exactly where he needs it, exactly when he needs it, no train wrecks.

In terms of spatial symmetries, this conservation law, the conservation of momentum, is a result of the fact that the boxcar example has no unbalanced horizontal forces. Other than the interacting boxcars, the tracks are clear. So moving forward or backward by a small amount does not uncover any unbalanced external force. This means the equations of motion have translational symmetry: a spatial translation forward or backwards changes the graph paper you would use for (x, y, z) coordinates, but it does not change the equations of motion. This is not the case for the prototypical accelerated vertical motion, free fall. In free fall, there is an external force, gravity; momentum is not conserved. But because this is true, free fall will help us view other conservation laws that exist.

Is there some other dynamical pattern or conservation law, perhaps temporal, that we can read from this chapter of the great book of the universe?

There is an additional conservation law, conservation of energy that we can see at work in free fall.  This is another reason that Galileo’s decision — to concentrate on studying free fall — has been such a helpful decision.

For our free fall example, we will go to the basketball court. A regulation NBA basketball has a mass of about . As it drops from a height, it acquires an additional of downward speed in every second of free fall. In terms of momentum, its momentum is not constant: it acquires an additional of downward momentum for each second of free fall. The following table lists out the momentum change.

The accounting in the table of Δp is second by second. It is temporal accounting.

Drop time (s)
	—	—

What if, in the spirit of Einstein’s theory of four dimensional spacetime, we try a different accounting method for the basketball in free fall, an accounting by spatial increments instead of temporal increments ? Let’s set it up.

Drop distance (m)
	—	—
		?
		?
		?

What kind of dynamical quantity, , comes in equal bites , meter for meter, in free fall?  It is not downward speed . It is not , the inverse of the downward speed. If one does a tiny bit of calculus and trigonometry, or if one hires an engineering major to do a tiny bit of calculus and trigonometry for one, then calculus shows two quantities come in equal size chunks when the free fall path is incremented spatially, meter by meter.
The first quantity is kinetic energy, , which depends on the speed and the mass, but slightly differently than momentum depends on speed and mass, viz.

The change in kinetic energy, , is equal for each meter of drop distance.

To calculate the kinetic energy at any drop distance, it is possible to use concepts we have already found:

That is a long and brain-burning calculation.  Yes, it is possible, but there is an alternate method that is much simpler.

Knowing the path and the force that causes , one can compute the work, , as the product of the force and the path, equal to the change in kinetic energy:

Note that in this equation, the value of must be , to encode the downward direction of the weight force, . So when is downward, or negative, the product is positive: kinetic energy increases as your object falls downward. It speeds up. However, if is positive, an upward trajectory, the product is negative: the kinetic energy decreases. It is getting slower on the way up.

Work: The definition of work is the change in the kinetic energy, , in which represents the axis along which the force acts.  So could represen the x-axis, the y-axis, the z-axis or even a slanted line.

The change in kinetic energy, , is equal for each meter of drop distance. Knowing the path and the force that causes , one can compute the work, , as the product of the force and the path, equal to the change in kinetic energy.

Drop distance (m)
	—	—

The second quantity that increments similarly, meter for meter, is the gravitational potential energy, , which we build from the work. If the work increments the kinetic energy equally, meter for meter, then we define the potential energy to be the opposite of the work done:

The minus sign in the above formula indicates “opposite of.”

So as work increases on the way down, the gravitational potential energy decreases by the same amount. Or, vice versa, on the way up, the work done on the basketball is negative, but the gravitational potential energy increases.  At higher altitude, the object holds that special form of energy, the potential for motion once it is free to drop and convert to kinetic energy.

For any spatial change, , the changes in kinetic energy and gravitational potential energy balance out:

This means that the sum must be a constant.  That constant is called the total energy.  We customarily use the symbol for total energy.  If total energy is defined as

then the conservation of energy, our second pattern, is simply this: “Total energy of a system is a constant.”

On a generic path, an object might be subject to a net force that has

• some Newtons, 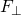, that are perpendicular to its displacement and to its velocity 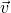, and
• some Newtons, 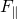, that are parallel to the velocity.

In this figure, the path has a tangent line (red dashed line) at point P.  The velocity at point P is along the tangent line.   is a curved path, so there are some Newtons of force centripetal to the path, . Let’s say that the net force also has some Newtons of force parallel to the path, . It is that increases the speed and the kinetic energy. The centripetal component cannot alter the kinetic energy, only the direction of motion.

This gives us the final version of the work equation:

where represents a small increment of a generic path that is not necessarily oriented to the x-, the y- or the z-axis.   is parallel to that small path increment and to the velocity vector.

What is the symmetry principle that corresponds to conservation of energy?

The symmetry principle behind the conservation of energy is a translation symmetry. However, it is not a spatial translation, between to points on a piece of graph paper, or two points on a road map. Instead, it is a translation in the temporal direction. If a small translation forwards or backwards in time does not change the equations of motion, energy will be conserved. One of the informal ways of failure of conservation of energy is for the system to have some friction forces at work. Friction forces unalterably dissipate energy as heat, as you know when your rub your palms together briskly. So thermodynamical considerations come into play for a full examination of time translation symmetry, and it is thermodynamic concepts that we discuss in Chapter 6.

About stopping time and stopping distance calculations

In general, it is handy to use

• the impulse formula, 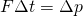, to get a stopping time , and
• the work formula, 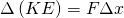,  to get a stopping distance .

Sometimes you have initial information about initial momentum and initial kinetic energy, and sometimes you have to put them together from definitions and .

Examples

The following examples give you a good idea of how to think through a few of the more difficult problems and calculations. I have worked out each example with step-by-step detail. Remember: the objective for this or just about any other science course is to learn how to think about the given topics. In this course, our given topic is Galileo’s “grand book” — the physical universe.

Example 1. Kansas City boxcars

A set of five boxcars interact in the Argentine freight switching yard in Kansas City.

Boxcar X is moving right at speed . The other four are hooked together and at rest. Each freight car is loaded to 90,000 kg. When boxcar X collides with the other four, it hooks in and all five boxcars move off to the right (not pictured) at a new speed, . Calculate the new speed, .

SOLUTION:

Boxcar X has of speed, so its momentum is…

Also, the diagram shows it moving rightward, so we can use a positive number to indicate the direction of .  Before collision, all of the momentum of the system is in boxcar X, and there is no momentum in the other four boxcars — they are at rest. Therefore the total momentum of the boxcar system is .

After interaction all of that is shared equally by each boxcar, but now they are linked together as a string of five boxcars, so they move at the same speed, . The total mass of the new string of five boxcars, moving as one unit, is .

Therefore,

You can cancel units of on left and right sides, then divide both sides by .  That is,

.

It is interesting to think about the interaction of boxcar X as it contacts boxcar U. They exchange equal but opposite momenta, and , mediated by the second law pair, and its opposite,  , for which the third law means that

As always, the minus sign signifies the opposite direction. The force from boxcar U on boxcar X, , has an unspecified size in this example, but we can at least say that its direction must be leftward. A leftward force on a boxcar that is moving to the right will slow down the boxcar. And the speed of boxcar X does indeed dip to from .

Similarly, the force of boxcar X on boxcar U, , and therefore on the other three, as well, is a rightward force. A rightward force on a boxcar at rest will accelerate it to the right. It is the same amount of force that cuts boxcar X by to , but it is only enough force to boost the other four boxcars from rest up to .

Example 2. Kennedy half dollar stopping distance

You observe a Kennedy half-dollar coin, of mass , sliding a cross a very smooth tabletop. Its initial kinetic energy is .

If the friction force between coin and tabletop is 0.09 N, then calculate the stopping distance.

SOLUTION:

First easy step: get that mass into kilograms!  We want to calculate in meters, seconds, kilograms, Newtons, Newton meters and Joules. Remember: a Newton meter, , is the same as a Joule, but is sometimes handier than for eventual cancellations. As for the mass: Since , so .

The initial kinetic energy, , must be dissipated by the friction force of size .  To stop the coin, its kinetic energy must dissipate down to zero, so . Therefore the change in kinetic energy, , i.e.,

or, more conveniently, .

We now have everything ready for the work formula.  For convenience we will consider the coin’s motion to be along the x-axis, and the friction for to be in the opposite direction.

Note that, using instead of Joules, I can now easily spot that Newtons cancel, left and right!  Also, the negative signs cancel, left and right. Excellent. The last step is to clear the right side of the equation with division by .

Therefore the stopping distance, , to three significant figures, is .

Side note: in this problem, you did not have to calculate the initial kinetic energy. It was in the starting information.

Example 3. Kennedy half dollar initial speed

You observe a Kennedy half-dollar coin, of mass m = 11.34 grams, sliding a cross a very smooth tabletop. Its initial kinetic energy is 0.12 J.

Calculate the initial speed of the Kennedy half dollar.

SOLUTION:

This problem requires that you use the kinetic energy definition,

then break it down in order to figure out and then itself. We have already converted the mass to kilograms, .  This time, however, we will use for Joules, by the same strategy as the previous example: that it will become convenient for later cancellations. That is,

So, let’s plug what we know into the kinetic energy definition:

the mass unit of kilograms cancels left and right, viz.,

On the left side, the remaining measurement units are , and on the right side is the square of a speed, . This means that, in terms of units, the left and right sides are consistent — good! The next step is to clear the right side with division by .

That is , so we must take the square root to get itself:

Therefore, the initial speed ..

Example 4. Kennedy half dollar stopping time, with check.

Now we can to a stopping time calculation with this Kennedy half dollar, because we have calculated its initial speed.  However, in other problems, you might have the initial speed or the initial momentum stated.  Read carefully.

Our task: calculate the stopping time of this Kennedy half dollar under a friction force .

SOLUTION:

We want to use the impulse formula, , in which we know the force, friction , but we do not know , although we can definitely put together.  Let’s start with the initial momentum, .

The final momentum, is zero: the coin has stopped.  Now we can calculate ,

Now we can plug what numbers we have into the impulse equation.

Note that I have changed the friction force units from to , for handy cancellations. Let’s cancel

1. negative signs,
2. mass units ,
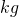3. distance units 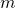and
4. one unit of .

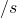Then we clear the left side with division by on both sides:

Remember: division by a fraction is the same as multiplication by the inverse of the fraction.  Therefore

Now we are finished: the stopping time is .

Check, using distance triangle formula

It is permissible to use the simple distance triangle formula, when an object is speeding up from rest or is stopping from an initial speed.  We have that in the Kennedy half dollar situation. It stops from an initial speed of , in a stopping time of .  But what is the acceleration, ?

Newton’s second law, especially the form , will help us get .

Now we can check our first example, but using the distance triangle formula.  Does it calculate out to ?

Nice!  It checks out.

This method with Newton’s second law and the distance triangle formula is an alternate method to calculate a stopping distance.  However, using the work formula is easier!

Example 5. The 2016 Bumblebee Camaro

You observe a 2016 Bumblebee Camaro take off from the starting line and drive a quarter mile () in 12.5 seconds flat. Its mass is , and its speed at the quarter mile mark is .

Calculate the average net force on Bumblebee during the 12.50 sec of the quarter mile.

SOLUTION:

The quarter mile sprint, for the 2016 Bumblebee Camaro, takes 12.50 seconds, reaching , or . The strategy is to calculate the acceleration and then the Newton’s second law net force. There are two separate ways to calculate an acceleration from the given information about the quarter mile.

1. Using distance triangles: Use the distance triangle formula, .
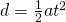   We know the quarter mile distance and the quarter mile time from the information published by GM. So, we can use the distance triangle formula to get the acceleration by the “back door”.

      

      

      

      

   Plug that acceleration value into 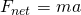to get the average net force on Bumblebee:

      

   The average net force is approximately .

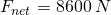2. Using the definition of acceleration: Use 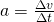, which, in this case is particularly easy.

      

      

   Note: this result is an average acceleration. Also note that this calculation uses no distance measurement. Another plug in

      

   gives the result, in this method, that the average net force is approximately .

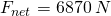Comments on the Bumblebee calculations

Why are the accelerations and net forces so different? One way to view the difference is to think about the measurement methods in this quarter mile test. A quarter mile straightaway is measured carefully by a surveyor, and that is used by the driving test team as a given, set piece of information. Also, the vehicle itself comes with a built in speedometer, and the test team probably added a second, really accurate speedometer, for its measurements. For their analysis, they did not rely on the built in speedometer’s measurements.

Because there are two independent measurements for the two different acceleration formulas, there is the possibility that the two acceleration values disagree even if if the speed, time and distance measurements are accurate. The definition of acceleration actually calculates an object’s average acceleration between two instants of time, but it has nothing valid to say about the instantaneous acceleration at any given instant of time between and . This is like the tortoise and hare problem: the instantaneous speeds and accelerations of the tortoise and hare vary significantly during the race. On the other hand, the distance triangle formula assumes that an object has a constant acceleration. That is, constant acceleration means that the slope of the distance triangle is constant. This is a good elementary view, and useful for calculus, but not every system accelerates smoothly.

For these reasons, you may say that the definition of acceleration, yielding an average acceleration, ignores variations in acceleration, and that the distance triangle formula forces an unvarying acceleration upon the calculations. A real automobile, however, might not have a smooth acceleration for an entire quarter mile, from zero to final speed . Depending on the transmission and driver, the vehicle might have more acceleration in the first few seconds, then slack off at higher speeds. The driver could tell you about it. And the driving test team can also tell you about it, because they probably use onboard accelerometers, like the accelerometers built into your smart phone, to measure the Bumblebee Camaro’s acceleration accurately every tenth or hundredth or thousandth of a second.