Main Body
Chapter 3, Dynamics: Sir Isaac Newton’s theory of why the states of motion change
brueckner

In the mind of Sir Isaac Newton, a force was the action applied to an object that changes the object’s state of motion from an inertial state, either rest or constant velocity, to a new state or a series of new states — an accelerated motion. Each of his three laws of motion is about force.
What is Newton’s first law of motion?
Newton’s first law of motion is a restatement of Galileo’s law of inertia, the property of indifference to being at rest or in a state of constant velocity. Newton described it as a resistance to changes in the state of motion unless some unbalanced force acts on the object.
An interesting way to understand this law is to take a trip on the UCF shuttle bus. As it accelerates across its path, in and around campus, it speeds up, slows down, turns left and right. If you are standing in the aisle, you have to stabilize yourself by holding onto the various grab bars.

If the bus is moving forward at constant speed, you can stand without bracing yourself. But as soon as it turns right, you will have to stabilize laterally or bump your left hip into the seat next to you. You are not bolted down to the bus, so you are indifferent to the forces turning the bus rightward: you want to keep going straight ahead. But the bus, and the seat bolted down to the bus, do turn right, bringing your left hip into a collision with the seat to your left. If the bus turns left, your right hip then is prone to getting bumped, unless you can stabilize yourself with one of the grab bars. Locking onto a grab bar fixes your position in the bus, something like the bolts do that hold the seats in place on the bus.
This effect, your body’s indifference to the forces acting on the bus, also holds for acceleration fore and aft. If the bus is moving forward at constant speed again, and you, again are standing in the aisle without locking to a grab bar, and the bus slows down, you’ll get thrown forward unless you brace. Your body wants to continue in that forward direction at constant speed, so, without locking onto a grab bar, you are prone to bump into the person in the aisle in front of you. If the bus speeds up, you are similarly prone to bump into the person behind you. So the law of inertia, Newton’s first law of motion, can be a good way to meet people, but it can also lead to bruises, unless you put a stone cold lock on those grab bars.

A more serious example of the law of inertia is the horrible effects of whiplash in a car accident. A person’s head can get whipped forward in a front end collision or backwards in a rear end collision, because the seat belts only anchor the torso to the car. The head is still free to move in any direction, which is good for normal driving but not in a collision. This is the reason that automobiles now have very carefully engineered head restraints and airbags. Professional race car drivers wear fancy head and neck support (HANS) devices for extra safety in a high speed collision.
Every object has its own measure of inertia, as measured in grams or kilograms of mass. Newton encoded the mass, the quantitative measure of inertia, into his second law.
What is Newton’s second law of motion?
Following Galileo, Newton conceived that the change in the state of motion was resisted by the mass of the object, so that a force of a given size acting upon a 2 kg mass would change the velocity at a certain rate, but that the same force acting on a 4 kg mass would change the velocity at only half that rate. That is, in mathematical terms, the acceleration must be inversely proportional to the mass and directly proportional to the net force.
![]()
One can also express this law in a more compact way:
![]()
This additional version of the second law allows us to define the unit of force in the metric system. Force has the units of mass with acceleration. A force that accelerates a 1.00 kg mass at an acceleration of 1.00 m/s2, is defined as 1.00 Newton of force.
![]()
This also permits us to calculate the weight force for anything on or near the surface of Earth, where the downward acceleration almost everywhere is ![]() . The minus sign here means vertically downward. Therefore a 1.00 kg mass has a weight force of 9.8 N, downward. In general, the weight force W of an object of mass m is
. The minus sign here means vertically downward. Therefore a 1.00 kg mass has a weight force of 9.8 N, downward. In general, the weight force W of an object of mass m is
![]()
It is customary to use the symbol ![]() or
or ![]() for the weight force, but be careful when we introduce other terms, like watts of power, which also use the symbol W.
for the weight force, but be careful when we introduce other terms, like watts of power, which also use the symbol W.
The customary American unit of force is the pound or pound-force. For this course, we will almost always use the metric unit, the Newton.
How do the directions of forces apply to accelerations in Newton’s second law?
To understand the directionality of accelerations, one must distinguish three vectors: velocity, acceleration and force.

“ANDRA Drag Racing Top Fuel at Perth Motorplex”by ANDRA Drag Racing is licensed under CC BY-NC 2.0
On a drag strip, a top fuel dragster rips up to new velocity states at a high rate, from a state of rest, accelerating across the quarter mile track in 4.4 seconds. That is an acceleration of about ![]() , a little more than four g’s of acceleration. The acceleration is in the direction of motion, down the track. One could also say that velocity (yellow arrow) and acceleration (red arrow) are parallel. Newton would then say that a force acted on the dragster in this same direction, forward.
, a little more than four g’s of acceleration. The acceleration is in the direction of motion, down the track. One could also say that velocity (yellow arrow) and acceleration (red arrow) are parallel. Newton would then say that a force acted on the dragster in this same direction, forward.
When the space shuttle pops its ‘chute and hits its brakes, the acceleration opposes the motion. The slowdown acceleration (red arrow) is antiparallel to the velocity (yellow arrow). Newton would then say that the slowdown force acting on the space shuttle is aft, in the same direction as the slowdown acceleration.

The Space Shuttle Endeavour’s drag chute deploys to slow the orbiter as it rolls out on Runway 22 at Edwards Air Force Base at the conclusion of its 14-day STS-111 mission to the International Space Station. June 19, 2002
NASA/Photo Jim Ross
How do two forces in different directions in two or three dimensions affect the acceleration of an object?
If two forces act on an object, but in opposite directions, then…
If two forces act on an object, but in opposite directions, then
- they are equal in size, or
- one of them will be stronger.
If they are the same size but opposite directions, then they balance each other, and the net effect on the motion of the object will be zero. The diagram below illustrates this, two equal forces in opposite directions, ![]() and
and ![]() .
.
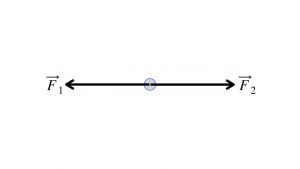
We could, for example, say that each force is 360 N. Then one could express the forces with numbers in this manner,
![]()
![]()
and the net force, the sum of the two force vectors, one could express in this manner:
![]()
If the two opposing forces are different sizes, then the net effect on the motion of the object will be in the direction of the larger force. The size of the net force is simply the amount by which the larger exceeds the smaller. The diagram below illustrates two opposing force, ![]() and
and ![]() , of different sizes.
, of different sizes.
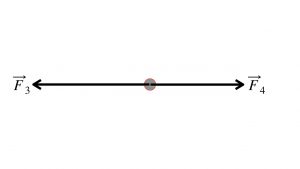
For example, if force F3 is 600 N to the left, and force F4 is 400 N to the right, then force F3 exceeds force F4 by 200 N, leftward. Therefore the net force Fnet = 200 N, to the left. That is,
![]()
As before, a negative number here stands for a leftward quantity: in this case, a leftward force of 200 N.
If you are working in one dimension, either
- left to right, along the x-axis, or
- up and down along the y-axis, or
- east and west out on University Boulevard, or
- north and south along Alafaya Trail,
then it is helpful to assign a negative sign to one direction, then add up the forces like positive and negative numbers. In the example of vertical free fall, the acceleration is downward, so ![]() gets a negative number:
gets a negative number: ![]() . The weight force of a 5.0 kg box of hammers gets a negative number, too:
. The weight force of a 5.0 kg box of hammers gets a negative number, too:
![]()
The value of ![]() is customarily listed as
is customarily listed as ![]() a positive number. However, depending on the context of your study, you might want to attach a negative sign to it,
a positive number. However, depending on the context of your study, you might want to attach a negative sign to it, ![]() if it is important to distinguish up from down. Read carefully and work carefully.
if it is important to distinguish up from down. Read carefully and work carefully.
If two forces act on an object, but in two different directions then…
If two forces act on an object, but in two different directions then the resulting acceleration will point in a combined direction determined by the diagonal of a parallelogram for which adjacent sides correspond to the direction and relative sizes of the two forces. Here’s how to sketch it out on graph paper:
- Draw in each force vector, tail-to-tail; the tail of each force vector is at a point.
- They each form one side of the parallelogram.
- Then trace in the rest of the parallelogram, like the dashed lines below.
- The diagonal of that parallelogram is the net force vector (in red).
- It is fairly easy to make a sketch like this on graph paper.
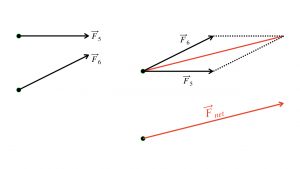
Let’s say, for example, that force ![]() pushes with 1.00 N to the right, and that force
pushes with 1.00 N to the right, and that force ![]() pushes 1.00 N to the right and 0.500 N upward; its slope is
pushes 1.00 N to the right and 0.500 N upward; its slope is ![]() .
.
This object, under the action of force ![]() would accelerate to the right. Similarly,
would accelerate to the right. Similarly, ![]() would, by itself, accelerate the object up and to the right, as shown, along a line with a slope of
would, by itself, accelerate the object up and to the right, as shown, along a line with a slope of ![]() . However, when acting together and for the same time interval, the resulting force, the net force,
. However, when acting together and for the same time interval, the resulting force, the net force, ![]() , is the diagonal of the parallelogram (red) formed by
, is the diagonal of the parallelogram (red) formed by ![]() and
and ![]() . The slope of the net force is therefore
. The slope of the net force is therefore ![]() , with a combined 2.00 N of force rightward and 0.500 N upward. One can then compute the size of the net force by using the Pythagorean Theorem, given that the net force forms the hypotenuse of a right triangle that is 2.00 N across and 0.500 N tall.
, with a combined 2.00 N of force rightward and 0.500 N upward. One can then compute the size of the net force by using the Pythagorean Theorem, given that the net force forms the hypotenuse of a right triangle that is 2.00 N across and 0.500 N tall.
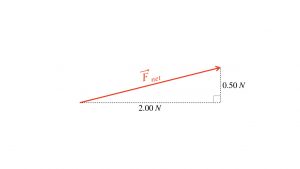
![]()
Therefore, the size of the net force is the square root of ![]() , or
, or ![]() , viz.
, viz.
![]()
Dragster example
As another example of using the second law, let’s use the top fuel dragster, mentioned above. At the start of the race, it has a weight force acting upon it and a forward force from the friction between tires and pavement. If the mass of the dragster is 1000 kg, then its weight force is downward and its size is
![]()
Horizontally, with acceleration ![]() down the track, its forward force is
down the track, its forward force is
![]()
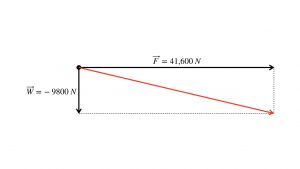
Perhaps you have noticed a slight flaw in this description of the dragster’s forces. If it has a downward weight force of 9800 N and a forward force of 41,600 N, then shouldn’t the net force drive it down into the ground?
We know this does not happen on a drag strip. The dragster does not trench itself into the track. But how does one explain this lack of a disastrous attempt to dig into the drag strip?
What are the signs of balanced forces?
The dragster does not dig into the surface of the track because the track is not made of liquid water. It is made of tough, rigid concrete and asphalt. These materials provide an upward rigidity force that balances the weight force.
Why use liquid water as an example of what a race track is not? A surface of liquid water, like swimming pool, could support a mosquito but not a dragster. The dragster would sink in the water, down to the bottom of the pool. Until mosquitoes develop tiny dragsters, there will be no drag strips on any pool of liquid water, because its rigidity force is insufficient.
The drag strip made of concrete and asphalt, however, is hard as the proverbial rock: it can support the 1 metric ton mass of the dragster.
This rigidity force is really a result of the submicroscopic calcium-silicon-hydrogen molecules in the cement holding itself together. As the weight presses down on it from above, the molecules stretch a bit like a trampoline. A trampoline slings you back into the sky, and the molecules push the dragster vertically upward. This rigidity force is called the “normal” force, not because it is ordinary, but because mathematicians use the word, “normal” to denote perpendicularity to a surface.
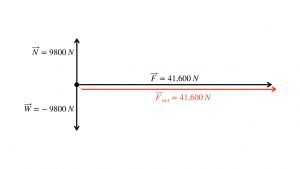
 for clarity.
for clarity.In this way, the normal force of the racetrack, due to its molecular bonds holding together, points perpendicular to the surface.

In the case of a dragster on a rigid race track or a coin on a table top or a warship floating in the Norwegian Sea, the sign of balanced forces is that the dragster, coin and warship do not change vertical position. Yet each object experiences downward Newtons of gravitational weight force. Therefore, it is fair for you to infer that the race track, the table top and the sea provide an upward force sufficient to balance the weight force.
Terminal velocity example
Another interesting example of balanced vertical forces is terminal velocity in free fall. In this case, we take into account the effects of aerodynamic drag on the skydiver. The skydiver jumps out of a perfectly good airplane, and his downward speed increases. As his speed increases, the drag force, “air resistance,” also increases.

In the skydiving image, above, the yellow dot represents the center of mass of the two skydivers. The faster the skydiver falls, the more drag force opposes his fall. This drag force is upward. As the skydiver’s downward speed increases, his upward drag force increases. However, his weight force ![]() is a set number of Newtons. Therefore, there will be a downward speed at which the upward drag force
is a set number of Newtons. Therefore, there will be a downward speed at which the upward drag force ![]() is so large that it exactly balances the downward weight force, Newton for Newton. When the skydiver hits that speed, the upward drag force and the downward weight force balance — acceleration vanishes, his velocity stops changing. It is the terminal velocity. Until the skydiver pops his ‘chute, that will be his downward speed.
is so large that it exactly balances the downward weight force, Newton for Newton. When the skydiver hits that speed, the upward drag force and the downward weight force balance — acceleration vanishes, his velocity stops changing. It is the terminal velocity. Until the skydiver pops his ‘chute, that will be his downward speed.
Uniform circular motion is a variation of accelerated motion in two dimensions.
In the boot heel of Italy, in the town of Nardo, is a large circular test track, the Nardo Ring, which many European automakers use for testing their vehicles at high speed.
Its radius is approximately 2.0 kilometer. Each lane of the track is banked, and the outer lane is banked sufficiently for a vehicle to travel at a constant speed of 66.7 m/s, or about 149 mph, without having to crank the steering wheel a single degree left or right. This is an example of motion in two dimensions that is accelerated, but without a change in the speed. The only change in the velocity is the change of direction of the velocity vector as the vehicle goes around the track.
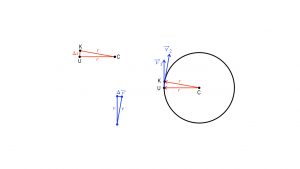
Because the vehicle neither speed up nor slows down, the acceleration is neither parallel nor antiparallel to the path, not even by a tiny amount.
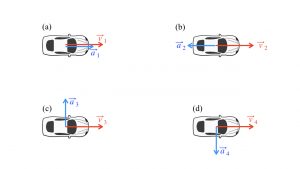
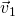 is parallel to acceleration
is parallel to acceleration 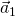 , the car is speeding up; (b) Velocity
, the car is speeding up; (b) Velocity 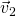 is antiparallel to acceleration
is antiparallel to acceleration 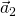 , the car is slowing down; (c) velocity
, the car is slowing down; (c) velocity 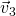 is perpendicular to acceleration
is perpendicular to acceleration 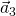 , which points to the car’s left, and the car is turning left but its speedometer is unchanging; (d) the Nardo Ring situation, velocity
, which points to the car’s left, and the car is turning left but its speedometer is unchanging; (d) the Nardo Ring situation, velocity 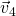 is perpendicular to acceleration
is perpendicular to acceleration 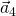 , which points to the car’s right, and the car is turning right but its speedometer is unchanging.
, which points to the car’s right, and the car is turning right but its speedometer is unchanging.Instead, the acceleration is perpendicular to the path, perpendicular to the instantaneous velocity vector. On the Nardo Ring, vehicles travel clockwise, so the direction of the velocity vector is always changing rightward, even though the steering wheel is in “neutral” position. With the ![]() vector pointing rightward, it is effectively pointing at the center of the Nardo Ring — it is centripetal.
vector pointing rightward, it is effectively pointing at the center of the Nardo Ring — it is centripetal.
Dynamically speaking, the acceleration on a circular path at constant speed is centripetal.
You can use proportional triangles to figure out the size of the centripetal acceleration, ![]() . For instance, on the circle with center point C, below, look at two positions a few degrees apart on the circle. On the Nardo Ring at 149 mph, you will have traveled about two degrees in one second of travel, so let’s consider the two positions to be ten degrees apart on the circle, about 5 seconds of elapsed time.
. For instance, on the circle with center point C, below, look at two positions a few degrees apart on the circle. On the Nardo Ring at 149 mph, you will have traveled about two degrees in one second of travel, so let’s consider the two positions to be ten degrees apart on the circle, about 5 seconds of elapsed time.
Let’s stand at the westernmost point of the ring, point U, and start our clock at time ![]() , and make our second position measurement at time
, and make our second position measurement at time ![]() . Therefore, at time
. Therefore, at time ![]() , the velocity arrow
, the velocity arrow ![]() is straight north; at time
is straight north; at time ![]() , the velocity arrow
, the velocity arrow ![]() is ten degrees right of that, as shown. Similarly, position vectors
is ten degrees right of that, as shown. Similarly, position vectors ![]() and
and ![]() are also 10 degrees apart. For an easy view, look at the red position triangle and the blue velocity triangle. They are isosceles triangles, though one is measured in meters and the other in meters per second. The long side of the position triangle is the radius
are also 10 degrees apart. For an easy view, look at the red position triangle and the blue velocity triangle. They are isosceles triangles, though one is measured in meters and the other in meters per second. The long side of the position triangle is the radius ![]() of the Nardo Ring; the long side of the velocity triangle is the uniform speed
of the Nardo Ring; the long side of the velocity triangle is the uniform speed ![]() on the car’s speedometer. Because they are isosceles triangles, and because the sharp acute angle on each is 10 degrees, the two triangles are proportional. The proportionality ratios are therefore
on the car’s speedometer. Because they are isosceles triangles, and because the sharp acute angle on each is 10 degrees, the two triangles are proportional. The proportionality ratios are therefore
![]()
In this expression, the ![]() represents the change in velocity between
represents the change in velocity between ![]() and
and ![]() . It forms the small blue base of the velocity triangle.
. It forms the small blue base of the velocity triangle.
Also in this expression, ![]() represents the change in position along the slightly slanted line segment from point U to point K. Because the two instants of time,
represents the change in position along the slightly slanted line segment from point U to point K. Because the two instants of time, ![]() and
and ![]() , are so close together, this straight line segment is very close to the exact distance along the arc of the actual circular path. This approximate length, in meters, is
, are so close together, this straight line segment is very close to the exact distance along the arc of the actual circular path. This approximate length, in meters, is ![]() . This allows one to modify the proportion,
. This allows one to modify the proportion,
![]()
Cross multiplication gets the familiar definition of acceleration, ![]() , on the left hand side,
, on the left hand side,
![]()
and the formula ![]() on the left. This means that the formula for the centripetal acceleration in uniform circular motion is
on the left. This means that the formula for the centripetal acceleration in uniform circular motion is
![]()
and that the formula for centripetal force is
![]()
It is important to note that these results are based on the geometry of the path, not on the specific nature of the force that provides this acceleration. Another way to state this is that the centripetal force formula applies to a gravitational force, like the force of gravity from Earth that keeps our moon on its orbit, or an electrical force between an electron and a proton in an atom of hydrogen.
Sir Isaac Newton used this geometric result as leverage to figure out his law of universal gravitation. He made a conjecture about
- the interaction of Earth with an apple in free-fall and
- the interaction of Earth with our moon, also in free fall but on a circular path.
To get deeper into Newton’s law of universal gravitation, however, we must look carefully at his third law of motion, the law of action and reaction.
What is Newton’s third law of motion?
Whatever pulls or pushes another object is also pulled or pushed by that other object, in equal but opposite amounts.
A pair of skateboarders facing each other push off against each other, for example. Newton’s third law says that their push forces are equal, Newton for Newton, but in opposite directions. They stay in contact for a fraction of a second and accelerate backwards.
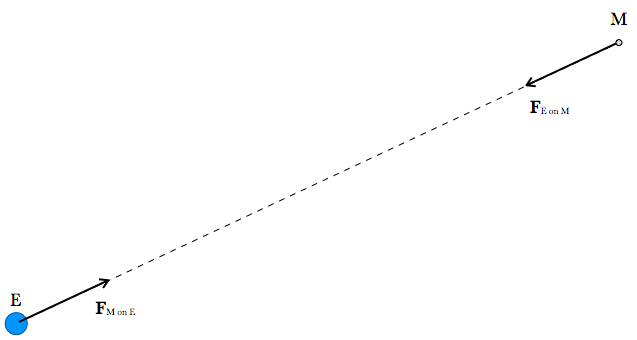
Another famous example is the force of gravitational attraction from the Earth on the moon, FE on M. It is a centripetal force, toward Earth, and it keeps the moon on its orbit with about 2 x 1026 Newtons of pull. According to Newton’s third law, the moon exerts the same size pull on Earth, FM on E, but moonward.
This idea, mutual interaction, rules the cosmos. Every dynamical system reveals its secrets to the scientist who sees it as a system experiencing interactions, from a seemingly simple system of skateboarders, to the celestial mechanics of the Earth/Moon system, and on down into the quantum world of electrons and photons, atoms and nuclei.
However, there is one caveat, even for the interaction of two skateboarders. When they push off from each other, with equal but opposite reaction, equal but opposite push forces, they do not necessarily move the same way, even though the forces are equal, Newton for Newton. You can ask yourself these questions,
i)“What is equal for both skateboarders?”
ii)“What is different between the skateboarders?”
iii)“Are their velocities the same or different?”
iv)“If Newton is correct with his third law, then what can I measure that will be the same amid the variations of skateboarders?”
The answers to these questions are the subject of the next chapter, in which we study the ideas of momentum and energy. Before we study those important concepts, let’s make a brief study of Newton’s greatest achievement, the theory of universal gravitation.

Credit: NASA, ESA, and the Hubble Heritage Team (STScI / AURA)
What orders the stars and planets?
Everyone looks up into the night sky, wondering at the stars. Why do they seem to march all night, along a circular arc, from eastern horizon at rising to western horizon at setting? Why does our moon circle Earth? As Galileo must have wondered when he first saw the moons of Jupiter, in the second week of January, 1610: what holds the Jovian moons in predictable orbits around Jupiter?
The ancient Greeks, Plato and his contemporaries, thought that a clear crystalline sphere circled around Earth, with Earth at its center, carrying the stars on their perfect circular paths. We still refer to this as the celestial sphere, a poetic turn of phrase but also useful shorthand for a stargazer — in which direction on the celestial sphere should one gaze to view the Big Dipper or Orion or the Great Spiral Nebula in Andromeda? In addition, each planet had its own sphere, nested inside the celestial sphere; the Sun and our moon also had their own spheres. These beautiful, idealized spheres were a sufficient explanation for Plato as to what orders the stars and planets.
Galileo made no great inquiry into what orders the stars and planets in their courses, but Sir Isaac Newton did so, as did Newton’s friend, Edmond Halley. Our study is about the theory of universal gravitation that Newton developed and which Halley applied so successfully.

What Newton knew
Terrestrial gravity
Newton and other scientists knew that the force of gravity on earth controls the tick tock of a pendulum. In his book, Principia, Newton describes a pendulum that another scientist, Christiaan Huygens from Holland, had set up in Paris, a pendulum design that ticks one second and tocks another second, so that its total period of repetitive motion was 2 seconds. They knew that the length of this pendulum was exactly the same as the drop distance for 1 second of free fall. In his book, Newton mentions the length of this pendulum,
A foot in Paris was not quite the same as a foot in England, but it was close. The pendulum in our lecture hall demonstration from March 2017 is almost this same length, 3 Paris feet and 8 lines ½, or 0.994 m. And it is not a coincidence that the drop distance of 1 second equals the length of a pendulum that ticks 1 second.
Measurements of Earth and moon in Newton’s day
In addition to full knowledge of Earth’s surface gravity, Sir Isaac Newton also knew the distance from the center of the moon to the center of Earth. From the days of the ancient Greeks, it had been estimated by triangulation that the Earth-moon distance was 59 Earth radii.

By Newton’s day, it had been measured a bit more precisely, 60.5 Earth radii. In his discussion of gravity, Newton decided to work with a round figure, assuming a mean distance of 60 Earth radii.
The rough size of Earth itself was also known to the ancient Greeks. By Newton’s day, French mathematician Jean Picard had made the best measurement of Earth’s circumference, 123249600 Paris feet, or, in modern units, 40,035 kilometers, which is just 0.2% above NASA’s modern value, 39,941 kilometers.
Newton also used a very precise measurement of the period of the moon’s revolution on orbit about Earth, 27 days, 7 hours and 43 minutes, or 27.3215 days, which is a few parts per million from NASA’s current value, 27.3217 days.
Moon’s centripetal acceleration
With fairly good measurements for earth’s size and the moon’s orbital parameters, Newton could make a very nice calculation of the moon’s centripetal acceleration from the force that keeps it on orbit.
![Rendered by QuickLaTeX.com \[a_{lunar}=\frac{v^2}{r}=\frac{\left[\frac{\text{moon's orbital circumference}}{27.3215\:days}\right]^2}{\text{moon's orbital circumference}}=\frac{\left[\frac{2\pi \left(60\,Earth\, radii\right)}{27.3215\:days}\right]^2}{\left(60\,Earth\, radii\right)}=\frac{\left[1018\frac{m}{s}\right]^2}{\left(382,300,000\:m\right)}\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-3a2f58db2291e184aa5858f8b73488f4_l3.png)
That works out to ![]() . “Big deal, a tiny acceleration, but so what?” you might think. What Sir Isaac Newton might have replied, after tossing his apple at you, is that, “Forsooth! It is almost exactly in the ratio
. “Big deal, a tiny acceleration, but so what?” you might think. What Sir Isaac Newton might have replied, after tossing his apple at you, is that, “Forsooth! It is almost exactly in the ratio ![]() with
with ![]() !” That is
!” That is
![]()
and Newton did not reckon it as a coincidence. Moon’s distance is 60 times greater, and its acceleration is 1/602 smaller. To Newton, it was no coincidence, but an important pattern in the numbers.
In fact, he estimated how far the moon would fall if you could hold it at its distance, 60 Earth radii away, and drop it like a mischievous child would drop a water balloon or like an apple dropping from an apple tree.
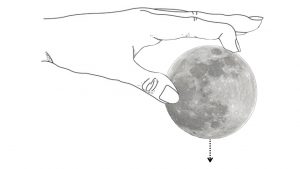
In one minute it would fall straight toward Earth a distance of 15’1″ in Paris feet and inches. In metric units, that is 9.80 m.
Newton’s conjecture
Building on this and other patterns from astronomical observations, Sir Isaac Newton developed his conjecture, that the force keeping the Moon on orbit is the same as the force dropping an apple to the ground in his garden. In Book III of his Principia, Newton writes his first statement of the law of gravitation in terms of the satellites of Jupiter, the “circumjovial planets” that Galileo discovered with his telescope:
This diagram shows Jupiter as we know it today, viewed from below and looking toward the North Star, and the closest of the circumjovial planets, the volcanic moon named Io. It is drawn to scale; Io is the yellowish dot on the right, very tiny compared to Jupiter itself.
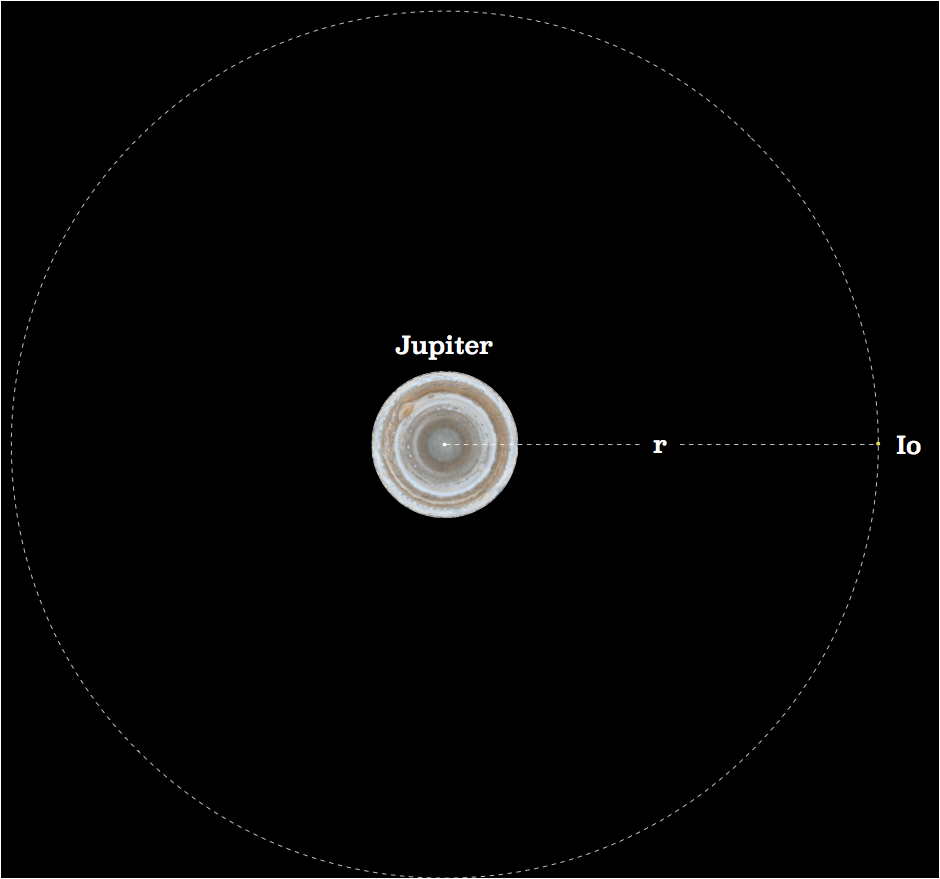
Comments:
- “Drawn off from rectilinear motion” implies the acceleration and force that curves a planet onto a circular orbit from the straight line motion it would have if there were no unbalanced force acting.
- “Toward Jupiter’s centre” is Sir Isaac’s way of stating it is a centripetal force.
- “Reciprocally as the squares of the distances” means that the formula has the square of Io’s distance, r2, in its denominator.
So the formula for the gravitational force might look like this,
![]()
But if so, how does one convert square meters in the denominator into Newtons of force? And what other physically measurable quantity might go into the numerator? A little bit farther in Book III, Proposition VI, Theorem VI, Corollary 2, Newton wrote,
Additional comments:
- “Weights of all” means the weight force, i.e., the force of universal gravitation.
- “At equal distances from the earth’s centre” means, e.g., at the surface of the Earth, about 6371 km above Earth’s center. Another example is at the orbit of the international space station, about 6800 km above the center of Earth, although, in free fall, everything behaves as if it is weightless.
- “As the quantities of matter which they severally contain” signifies the gravitational force is proportional to a measurable quantity, mass.
For this reason, we would place both the mass of Earth and the mass of the object — apple, astronaut or any other object — in the numerator of the formula… OR mass of Jupiter and mass of Io in the numeratory, viz.
![]()

and in general,
![]()
for any two masses, ![]() and
and ![]() .
.
Because the metric unit of force, the Newton, is kg m/s2, and because the formula’s measurements of mass and distance combine for kg2/m2, one must also have a multiplication factor ![]() , to convert kg2/m2 into kg m/s2. So
, to convert kg2/m2 into kg m/s2. So ![]() might be
might be
![Rendered by QuickLaTeX.com \[G=42\frac{N}{\frac{kg^2}{m^2}} \longrightarrow 42\frac{\frac{kg\:m}{s^2}}{\frac{kg^2}{m^2}} \longrightarrow 42\frac{kg\: m^3}{kg^2 \: s^2} \longrightarrow 42\frac{m^3}{kg\:s^2}\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-0c5da6e79b85ccbc0dab429be90ed795_l3.png)
or possibly some number other than 42. If you could measure the force between two 1.00 kg masses at a distance of 1.00 m, then you could figure out the value of ![]() .
.
The gravitational constant, G
This multiplicative constant, ![]() , is known as Newton’s constant or the gravitation constant. In 1774, English King George’s royal astronomer, Nevil Maskelyne, set out to measure the gravitational force of a lovely mountain in Scotland, Schiehallion, near Loch Rannoch (indicated by the red arrow)
, is known as Newton’s constant or the gravitation constant. In 1774, English King George’s royal astronomer, Nevil Maskelyne, set out to measure the gravitational force of a lovely mountain in Scotland, Schiehallion, near Loch Rannoch (indicated by the red arrow)
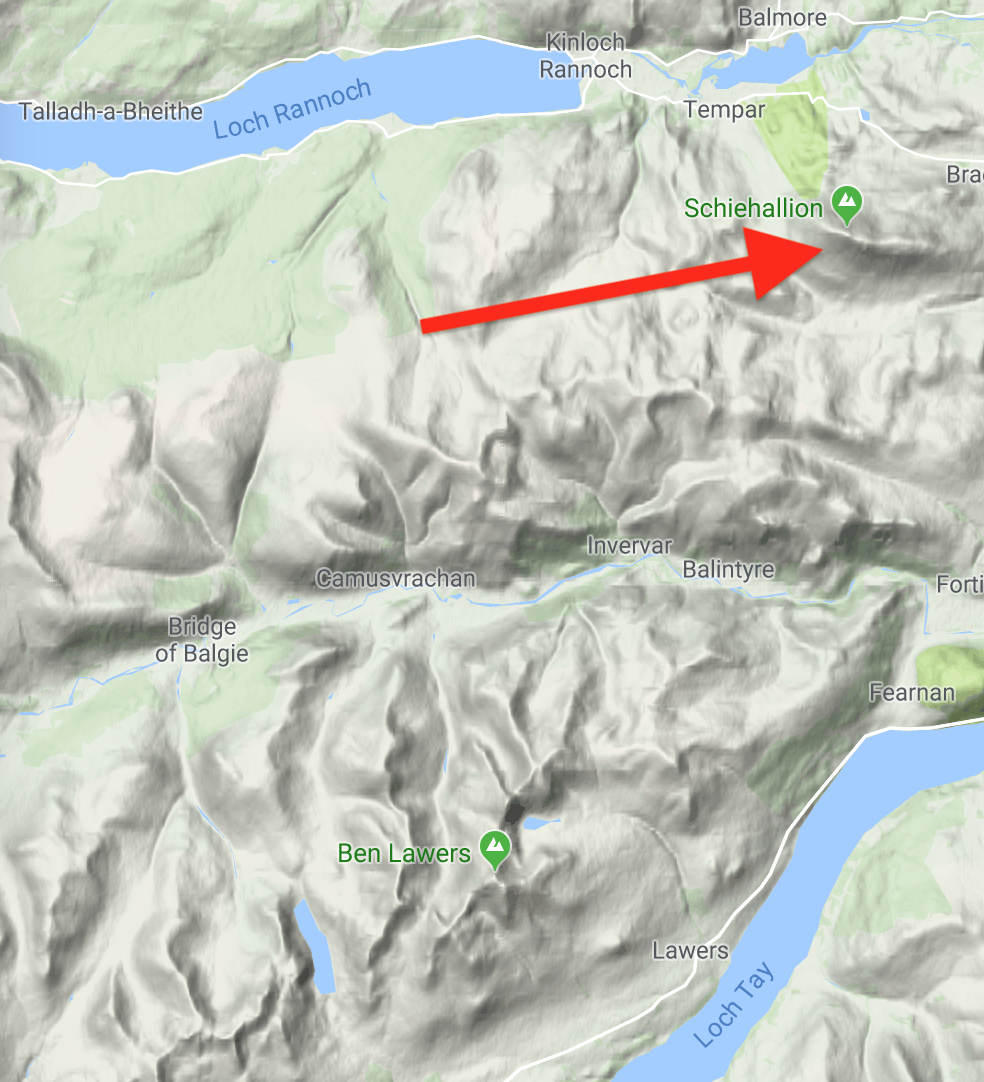
a mountain that is sufficiently symmetric that its volume can be easily calculated. Knowing the volume and the density of its rock, Maskelyne and his crew could calculate the mass of the mountain. Then they set up a pendulum close to the mountain, and measured its deviation from true vertical due to being pulled toward the mountain instead of straight down to the center of Earth. So m1 was Earth’s mass and m2 was Schiehallion’s mass.
A few years later, Henry Cavendish made a more precise measurement in his London laboratory, not using Earth and a mountain, but using large lead spheres and a very precise balance. Cavendish used his measurements to evaluate the density of our planet. From his results one could then get a value for G, and it was not 42.
![]()
That is fairly good, because today’s value of G, as published by the National Institute of Standards and Technology (NIST) is
![]()
The gravitational constant, G, is not just a conversion factor. It encodes the strength of the gravitational interaction in a way that has significance even in Einstein’s general theory of relativity. Among other interesting features of relativity, G controls the size of the event horizon of a black hole. The event horizon is the “point of no return,” inside of which nothing can escape the black hole, not even light itself. G specifies the number meters of event horizon size for every kilogram of black hole mass. For instance, our star, the Sun, would be a black hole if it could be squeezed down to a sphere of about 3 kilometer radius.
Halley’s prediction
Edmond Halley was a friend of Isaac Newton, and was the instigator who poked and prodded Newton into publishing his notes and studies about the gravitational system of the world, a publication known as the Principia.

“Portrait of Edmund Halley”by ancientartpodcast.org is licensed under CC BY 2.0
One of Halley’s many interests was comets and their precise orbits in the gravitational field of the Sun, according to Newton’s theory of universal gravitation. Halley thought that there were comets throughout the centuries that were not separate comets but the same comet making return visits to the inner solar system on an elliptical orbit. One of his comets was the comet of 1531, which he identified with the comet of 1607 and the comet of 1682. He predicted that this comet would return in the year 1758. It did return, about Christmas time in 1758. That comet is now known as Halley’s Comet. It continues to visit the inner solar system every 76 years. Halley and Newton had both passed away by 1758, but this astoundingly correct prediction was considered a giant verification of Newton’s theory of universal gravitation.
Newton’s theory is well verified to this day, and all scientists who develop a new physical theory must try to verify their theory by experiment and observation as Halley and Newton did 300 years ago.