Fiber optic internet, making water bend, lightning strikes

When you connect to a fiber optic network, as shown in the image above, the pulses of light stay inside the fiber and transport energy, momentum and information from #justinbieber updates on Instagram. Everything about the flow of information through the fiber optic network is electromagnetic, a complex but reliable interaction of light and matter.

When you take a regular party balloon and scuff it up along your shirt to get it all electrified with static electricity, you can make water bend from it free-fall trajectory, faucet to sink, by bringing the balloon close to the stream of water, as shown in the following photo.

And is it true that this balloon’s static electricity is the same kind as one sees in spectacular lightning strikes?

Yes, it is the same — for the party balloon, for the spectacular lightning strike, for your #justinbieberBFF data over the internet. It is all electromagnetic, the interaction of the electromagnetic field with matter.

Sub-microscopic view vs. macroscopic view

In the current day, long after Benjamin Franklin’s electrical experiments, long after Michael Faraday’s discoveries, long after James Clerk Maxwell developed his systematic equations, we take a very basic, modern view, that the simplest electromagnetic interaction at the sub-microscopic level boils down to an electron interacting with a photon.

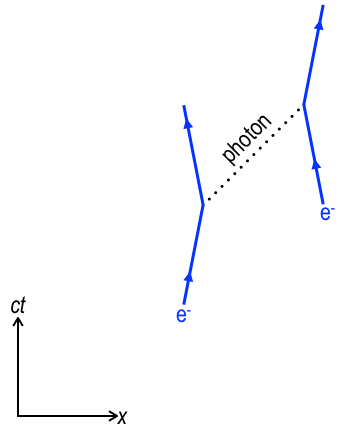
The electron, orbiting an atom’s nucleus, is a quantum particle, and so is the photon. This view of the interaction is called QED, quantum electrodynamics. In the diagram above, two electrons (e^–) repel through the exchange of a virtual photon (dotted 45°line). Scientists can draw a similar QED diagram for a proton interacting with a photon. We will speak more about quantum properties of photons, electrons and protons in the next chapter, but for now this simple diagram will suffice.

Electrons and photons are very small, so in a human-sized system, the numbers of photons and electrons are enormous. As an example, consider a white 60 Watt incandescent light bulb that is 20 meters from you, and you are in an otherwise darkened arena, like the CFE Arena on campus. If you recall your experiments with prisms in grade school, you know that white light is a mixture of all colors, from red to orange, yellow, green, blue, indigo and violet. In this darkened arena with one light burning 20 m from you, some red photons reach your eye along with photons of all the other colors. Each red photon has 3 x 10^-19 Joule of energy, a very small energy, and the energies of the other color photons are also in the 10^-19 Joule range. At twenty meters’ distance, where you are, the 60 Watts is spread out, diluted by distance, so that every square centimeter facing the 60 Watt bulb catches about 0.0000019 Joules of energy per second. With only that light bulb burning, the arena is fairly dark; if you were 1 meter from the light, you could read a newspaper, but at 20 meters reading the newspaper would be tougher. For this reason, the pupils in your eye will dilate to about 8 millimeter diameter, and its πr² area would be about half of a square centimeter. Therefore each eye catches maybe 0.00000095 Joules of photon energy per second. That translates to about 10¹² photons entering each eye. That is an enormous number, a trillion, if you had to count them. Even that dim light puts you in a veritable Mississippi River of photons. But the retina is happy as the proverbial clam to catch all of them, one electron jumping into action for each incoming photon, no sweat, followed by an electrical signal into your brain along the optic nerve about what you see.

Riding in a river of photons, though, we do not necessarily have to use QED for everyday applications. For everyday human-scale systems, instead of talking about 10¹² photons smoothly interacting with 10¹² electrons, we have a concept, the electrical field, that encodes the electromagnetic effect of that river of a trillion photons. We also have an everyday size electrical charge unit, the Coulomb. It is a metric system unit, defined with current-carrying wires, meter sticks and Newtons, and in terms of electrons, 1.00 Coulomb is the same size charge as the charge on 6.24 x 10¹⁸ electrons. Technically, however, electrons are considered negative charges, so

.

And protons in the atomic nucleus have the same size charge as an electron, except they are considered positive charges, so

.

The constant of nature associated with electrons and protons is the fundamental charge, e.

Thus, one might say that the charge on the proton is e and that the charge on the electron is -e. The customary abbreviation for the Coulomb unit is C.

Before we continue with human-scale electromagnetic concepts, it is important to note that the mass of the proton is much larger than the mass of the electron, about 2000 times larger. So in most human-scale electrical systems, light bulbs, smart phones and so on, the charges that move through a wire are electrons, not protons. However, in the fiery furnace of the surface of the Sun, where the temperature is about 5800 K, most atoms are stripped of one electron or more, so there are plenty of protons and other positive particles flying around in the huge current filaments you can see in NASA’s Solar and Heliospheric Observatory (SOHO) website, https://sohowww.nascom.nasa.gov.

Protons accelerate in the opposite direction to electron accelerations, and they are much more sluggish, due to their greater mass. But in your apartment or dorm room, it is the electrons that are moving.

Where do the electrons go?

When I was a lowly lab TA in graduate school, one of my students wrote a one-page paper, a “microtheme,” with the title, “Where do the electrons go?” At the time it struck me hard, as one of the fundamental questions a scientist wants to answer.  In order to savvy for an electron, one must ask, “What force acts on the electron, and how much mass does it have?”

We now start our answer to that question with a well-measured force law, developed by Charles Augustin de Coulomb, the French scientist of the late 1700s. He used a torsion balance, in which the balance arm stays level, suspended on a silver wire. The balance arm experiences torque about the silver wire, twisting a few degrees in a horizontal plane, like a merry-go-round at the park, all depending on the positive or negative charges Q₁ and Q₂ on the two small spheres in the device:

In this remarkable series of small twist angle measurements,

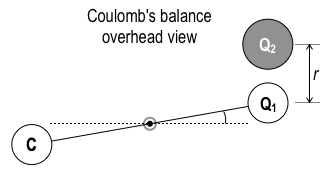
with two different charges, Q₁ and Q₂, a distance r apart, and with uncharged counterbalance C, Coulomb found that the electrical force has the same distance dependence as universal gravitation: the famous inverse r² dependence. We now call this the Coulomb force or the Coulomb interaction. Let’s write down the force law now, as an equation

It bears a strong resemblance to Newton’s law of universal gravitation, but it also has important differences, too.

1. Similarities:
   1. It is a pairwise interaction between two charges, Q₁ and Q₂, similar to gravity between two masses m₁ and m₂.
   2. It is inversely dependent on the square of the distance between centers of each charge. This means the photon is massless and gives the Coulomb interaction an infinite range.
   3. It has a conversion constant k, known as Coulomb’s constant, k = 9 x 10⁹ Nm²/C². Remarkably, k actually encodes the square of the speed of light, c².
2. Differences:
   1. The Coulomb force can be repulsive, between two positive charges or between two negative charges. Gravity is always attractive.
   2. The electric charge comes in two kinds, positive and negative. Gravitational mass, however, is a single kind, always positive. That is, an object can have an electric charge of -1.2 C, but it cannot have a mass of -3.08 kg.
   3. Electromagnetic fields can be screened, but gravitational fields cannot be screened.

When you walk into a building or a room where your smart phone cannot make a call, zero bars, then most likely you are inside a metal building of some kind. The name for a structure of this kind is Faraday cage. You can also see shielding if you slice through a coaxial television cable: a good copper conductor at the core for the actual television signal, then some insulation, then a braided metal “cage” to shield the core signal from interference by external electric fields such as a nearby appliance.

More subsections to be activated ASAP.  For now, use the YouTube lectures 26, 27, and 28.

Linear array of electrical charges

Relative strength of gravitational vs. Coulomb interactions

The electric field

Since the everyday scale unit of charge, the Coulomb, corresponds to such an enormous number of electrons or protons, scientists have found it helpful to abstract the Coulomb force between a pair of charges and render the electromagnetic influence outside an array of charge as the electric field, E. For instance, take a pair of parallel metal plates, equally charged but of opposite sign, -1.00 C on the upper plate and +1.00 C on the lower plate. It is easy to do this with a battery.

Now send in a singly ionized sodium atom (Na⁺), i.e., a sodium that has been stripped of its outermost electron. Going through this gauntlet, the Na+ ion will definitely feel an effect

from the veritable beehive of extra electrons above and

from the seething mass of protons below no longer balanced by electrons that are missing.

One might ask, “In what direction will that little Na+ ion get accelerated?” And it is certain that the sodium ion will not have much of a repulsive or attractive effect so as to make a significant rearrangement of the -1.00 C of extra electrons or the +1.00 C of unmasked protons. This being the case, we scientists use the electric field as a spacetime property of a given charge array, independent of whatever positive or negative charge, like our sodium ion, that you might send near the array. But where does the ion go?

Let’s figure out the direction of force on the Na⁺ ion. First, though the sodium ion will not drastically rearrange the parallel plates charge array, it might be possible for electrons to jump off the top plate and zoom down to the positive plate. After all, sparks and lightning do occur under the right conditions. However, the air between the parallel plates is a good insulator, a form of matter through which it is relatively difficult to move electrons, though not impossible. You have to build up a huge load of extra electrons in the belly of a thundercloud for that charge to jump across the air as a lightning bolt. A typical Florida lightning bold can convey on the order of 10²³ electrons to the ground in a fraction of a second. That is a big load. But generally, air is a fairly good insulator, so, lightning aside, let’s say that the ±1.00 Coulomb of charge in the plates is stuck in the plates.

However, they are metal plates, and metals are usually good conductors of current. That being the case, the extra electrons in the upper plate will move easily, repelling each other so that each electron’s net force is zero. The electrons do this by spacing themselves relatively uniformly.

To figure out the direction of the net force on the sodium ion, we will use the two ideas of “no jumping” between plates and “uniform spacing” of charges on each plate. Additionally, let’s break down the forces into those forces of repulsion from positive charges on the bottom plate and forces of attraction towards all the negative charge in the upper plate. If the ion is somewhere near the middle of the plates, as shown, then for every positive hunk of charge to its left, e.g., ΔQ₁, it will get some repulsion (red arrow) away from ΔQ₁, up and to the right, and similarly, there will be a hunk of charge ΔQ₂ spaced symmetrically to the right which will push with the same strength but symmetrically up and to the left. The two symmetric pushes cancel horizontally, so that the only Newtons of force that survive are the vertical net of these two force, as shown by the red upward net force arrow. The positive charges separate themselves uniformly, so for any other small hunk of charge on the left side, there will always be its symmetric partner in crime on the right half, resulting in a net upward force. This being the case, you can account for the entire positive array’s net force on the sodium ion: it’s upward.

Similarly, for the upper plate, symmetric chunks of negative charge pull the sodium ion upward, as shown by the blue arrows below.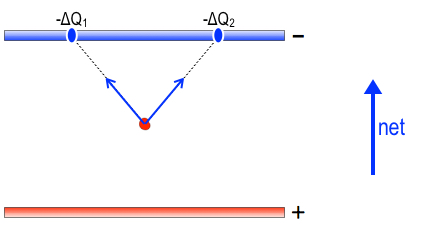

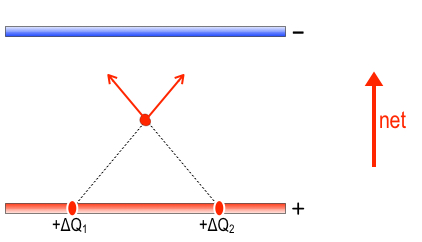It looks just like the diagram of positive charge forces, except it is an attraction, not a repulsion. The net force from these two negative chunks of charge is also upward. By virtue of uniform negative charge separation in the upper plate, one can see that you can always find two partners in crime up there, too, yielding net upward force from the entire upper plate.

In fact, the electric force is always upward between two parallel plates, posive below, negative above. If the plates are fairly close together compared to their width, then it is fair to say that the electric force is upward and of uniform strength everywhere between the plates except