Main Body
Chapter 6, Heat: The flow of energy and the direction of time



Water, air and temperature
If you take a quantity of water, place it in a cooking pot and turn on the heat, as in this photo, it will warm up and eventually boil. If you keep the heat on long enough, you will boil away all the water. But what happens to that water? Does it stop being H2O, two hydrogen atoms bonded with an oxygen atom? Or is it a gas, a vapor, floating around in the atmosphere? And why does a set amount of tap water, let’s say a quart of tap water, take less time to boil if the stove burner is set to “HIGH” than the same amount of water from the same tap but with the stove set to “MEDIUM” heat?




Why do thunderstorms form so often on hot, humid summer days in Florida, as in this photo, above, but not on equally hot days in April when the atmosphere is less humid? A good example from 2016 is the two days April 1 and May 17: high temperatures of 91º F, thunderstorms and over an inch of rain in Orlando on May 17, but no precipitation on April 1. Why was that?



When a hurricane approaches Florida, we listen to weather reports about the central pressure, maybe 900 millibars, we track the storm by satellite, as in this image, right, and we predict its path. But why do we fear elevated surface temperature in the Atlantic and the Gulf of Mexico?
We can apply our ideas of momentum and energy, force and acceleration to all of these questions about the thermal state of water and air. Our applications lead us to extract more advanced concepts like temperature, pressure and heat transport in this chapter.
Solid water, liquid water and gaseous water
The behavior of water at its freezing point and at its boiling point define the set points of the Celsius and Fahrenheit temperature scales.
| Phase transition of H2O | Fahrenheit | Celsius | Kelvin |
| freeze/melt | 32 | 0 | 273 |
| boil/condense | 212 | 100 | 373 |
The third common temperature scale, the Kelvin scale or absolute scale, will become especially important for us later in this chapter when we make calculations. With Fahrenheit and Celsius, however, these phase transitions of water are the anchors to the temperature scale.
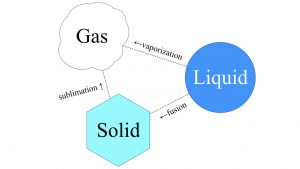
Phase transition is the scientific term for the process in which a liquid form of matter transforms to either a solid or a gas. The words we use for the phase transition from liquid to solid is freeze or solidify or fusion. For instance, a volcano’s molten lava flows like a liquid, but you wouldn’t really say it freezes, — you would say it solidifies. From liquid to gaseous state, that’s either boiling or vaporizing something. Solid matter can also go to the other two phases of matter, liquid and gaseous. Solid to gaseous phase transition is known as sublimation. That’s something that CO2, carbon dioxide, does under certain conditions. The polar ice caps of Mars are mostly CO2 ice. If you go to Publix and buy a big block of dry ice, carbon dioxide ice, it will not leave a pool of liquid when it heats up. That is sublimation. It will go directly to a gas. That’s why we call it dry ice.
Scientists have measured the freezing, boiling points and sublimation of many substances like gold, iron, CO2, H2O. Here is a short table of freezing and melting points for a few common substances, and, for reference, their densities in solid phase and a few densities in liquid phase. Gases are compressible, so their density varies with pressure and temperature, and they are not amenable to a short table. Note: ammonia is a gas at room temperature, although we purchase it at the supermarket as a bottle of aqueous solution. Also, the densities of liquids are measurements at the boiling point of each liquid.
An example of gaseous to liquid phase transition is water vapor in the atmosphere turning into droplets of rain. At the right altitude, the temperature and atmospheric pressure are just right for water vapor to condense into micro-droplets of liquid water. This forms clouds, a mist of micro-droplets that are so small, they are lofted into the atmosphere by thermal updrafts. That’s why thunder clouds build higher and higher, bigger and bigger. These micro-droplets collide and coalesce into bigger droplets. Eventually they become so big, possibly at a different altitude, and, again, where the temperature and atmospheric pressure are just right, thermal updrafts can no longer hold them aloft. They fall as rain. Whenever you see a cloud, you’re usually looking at liquid droplets of water that are still held aloft. An exception to that is a cirrus cloud, the really high, really wispy ones that look like strands of hair or horses’ tails. Those are actually ice crystals, and on a cold clear night, when the moon is full, ice crystals aloft form a set of rings around the moon, a lovely sight!
| Substance | Melting point (°C) | Boiling point (°C) | Density as solid (g/cm3) | Density as liquid (g/cm3) |
| H2O | 0 | 100 | 0.50 | 1.00 |
| Ethanol | -114 | 78 | — | 0.789 |
| Ammonia | -78 | -33 | 0.817 | 0.682 |
| Aluminum | 660 | 2519 | 2.700 | 2.375 |
| Iron | 1538 | 2861 | 7.874 | 7.124 |
| Copper | 1085 | 2927 | 8.920 | 7.992 |
| Silver | 962 | 2162 | 10.490 | 9.346 |
| Gold | 1064 | 2856 | 19.300 | 17.4 |
| Lead | 327 | 1749 | 11.340 | 10.678 |
| Note: ammonia is a gas at room temperature, although we purchase it at the supermarket as a bottle of aqueous solution. Also, the densities of liquids are measurements at the boiling point of each liquid. | ||||





One way to think about the three phases is the relative energy rankings. A gaseous material is going to have a higher average energy, atom for atom, molecule for molecule, than the liquid state. The solid state of the same material occupies the lowest of the average energy states. In the solid, the molecules have so little kinetic energy that they’re still stuck in a crystal lattice of some kind, either a diamond crystal or hexagonal crystals like ice, or any other kind of crystal that you may find.
Another factor that affects phase transitions is the ambient pressure. If you put some ribs in a pressure cooker, they cook to a state of tenderness much more rapidly than in a conventional oven or on a barbecue grill, and cooking is a way of making chemical reactions happen. Phase transitions in carbon dioxide display some interesting effects of ambient pressure. Dry ice actually can go to liquid, but only in high pressure environments. We call it dry ice because in normal atmospheric pressure at the surface of earth, it goes straight from solid to a gas. It sublimates. It doesn’t go through the liquid phase the way water does. But you can get solid to liquid to gas from CO2. In other words, you can get a CO2 puddle if the ambient pressure is high enough.
 |
 |
Pressure in a fluid and momentum states of atoms and molecules
The ancient Greeks thought of atoms but not molecules as we think of molecules today. In the 1700s scientists got more serious about the idea of atoms and molecules, and they developed the molecular theory and, as a subset, the kinetic theory of gases. Some of the assumptions of the kinetic theory of gases are
- that an everyday sized sample, i.e., a macroscopic sample like a balloon or a ballroom, has a very large number of particles in it, but that the particles are so small their separations are much larger than the particle size;
- that the particles move in random directions with a huge variety of speeds;
- that the particles do not experience long range interactions but interact by collision with each other and with the boundaries of the container like billiard balls;
- and that the particles obey Newton’s three laws of motion.
This set of assumptions is not meant to be exact and completely accurate, but it is close enough to a real gas that a scientist can use it as a shorthand version, an idealized gas model, from which it is easy to extract macroscopic averages, like a pressure.
The basic idea of pressure, one of a fluid’s measurable physical properties, is that it sums up the effect of all the atoms or molecules exchanging momentum with the sides of the fluid’s container. This diagram shows a perspective view and an overhead view of one such collision.
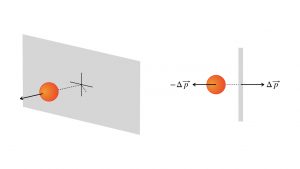
Each particle exchanges momentum ![]() with the wall. In one second, or during any time interval , there will be a huge number of such exchanges. That creates a net force on the wall,
with the wall. In one second, or during any time interval , there will be a huge number of such exchanges. That creates a net force on the wall, ![]() . And every square inch of the wall, every square centimeter, every square meter, gets a number of these exchanges per second, depending upon the density of the fluid. The pressure is the macroscopic measure of the average effect of all these submicroscopic collisions per square inch or square meter.
. And every square inch of the wall, every square centimeter, every square meter, gets a number of these exchanges per second, depending upon the density of the fluid. The pressure is the macroscopic measure of the average effect of all these submicroscopic collisions per square inch or square meter.
![]()
That is, pressure is measured in Newtons per square meter, one number that encodes the effect of many particles exchanging momentum with the wall at a given rate, per second, and at a given density, per square meter. In the metric system, 1.00 N/m2 is named the Pascal, abbreviated Pa, after the French scientist Blaise Pascal who developed the theory of atmospheric pressure and fluid pressures in general. In the customary English system, the pressure measurement is PSI, pounds of force per square inch. In the USA, bicycle and automobile tires have PSI ratings for inflation, about 50 PSI or so for a mountain bike’s tire, about 30 PSI for automobiles. This rating is the amount of extra pressure the air pump delivers above the atmospheric pressure. On television, the weather reports refer to the atmospheric pressure in millibars: 1.000 bar = 100,000 Pa; 1.000 millibar = 100 Pa.
The atmosphere of Earth has mass and weight, approximately 14.7 PSI, 101325 Pa, 1013.25 millibars at sea level on a fair day. Foul weather is usually a function of low atmospheric pressure. For example, a hurricane’s central pressure, in the eye of the hurricane, might be as low 880 millibars or even lower. A fair day in Denver, however, might be about 850 millibars, a lower atmospheric pressure because of the mile high altitude there. That is, the most dense layer of Earth’s atmosphere is below Denver and does not weigh down on Denver’s air.
The atmosphere, abbreviated atm, is another common pressure unit. Exactly 1.00 atm = 101325 Pa. A SCUBA diver might think in terms of atmospheres: every 10 meters of depth underwater adds another atmosphere of pressure from the weight of the water.
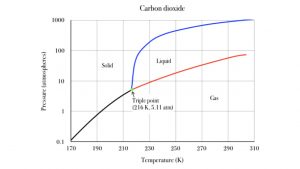
At normal atmospheric pressure, carbon dioxide ice sublimates to carbon dioxide gas. But at high pressure, it can melt to liquid carbon dioxide. The following graph shows the pressure and temperature conditions for sold, liquid and gas phases of carbon dioxide. The black line is the sublimation line. Pressure and temperature conditions divide along the black line, solid to the left of it, gas to the right. If you heat up your sample of solid carbon dioxide, its temperature moves to the right, across the black line, and the carbon dioxide sublimates to the gaseous state. The blue line is the melting line, separating solid from liquid states. Note that this transition only occurs at relatively high pressure conditions, above 5.11 atmospheres! That is over five times more pressure than our atmosphere provides. The red line divides liquid from gas: this is the evaporation line. Heating liquid CO2 from left of the red line moves it across to the gas phase. This is also a special pressure effect above 5.11 atm. The 1 atm line is quite a bit below the CO2 triple point.
The green triple point represents the unique temperature and pressure condition at which carbon dioxide is indifferent to solid, liquid and gas. They coexist at the temperature and pressure. Similarly, for water, solid and liquid H2O are thermally indifferent to each other when their temperature is 0°C. This is ice water! In a well insulated thermos container, which prevents heat energy from entering or leaving, the liquid grams of water will stay liquid for a long time, without freezing, and the solid grams of H2O ice will stay solid for a long time, without melting.
Temperature in a substance and kinetic energy states of atoms and molecules
The idealized concept of a gas being a collection of molecules also requires one to consider their kinetic energy states. Experiments by the chemist Thomas Graham in Scotland indicated that the rate ![]() at which a gas escapes through a small opening in its container, effusion, depends on the square root of the molecular mass
at which a gas escapes through a small opening in its container, effusion, depends on the square root of the molecular mass ![]() in the following way:
in the following way: ![]() .
.
In this expression, ![]() is a constant of proportionality. If one interprets the rate
is a constant of proportionality. If one interprets the rate ![]() as an average speed, then it is easy to relate this to the average kinetic energy:
as an average speed, then it is easy to relate this to the average kinetic energy:
![]()
So it is logical to expect to see the rate ![]() , like an average speed,
, like an average speed,
![Rendered by QuickLaTeX.com \[r=v_{avg}=\sqrt{\frac{2\left[KE\right]_{avg}}{m}}\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-99b9bfefe283cba02735b783a057b9fd_l3.png)
has a square root of the molecular mass m in its denominator. When you use a few trigonometric, calculus and statistics techniques, applying Newton’s laws carefully, you also find that the temperature is proportional to the average kinetic energy. The temperature-energy relation is quite simple:
![]()
where the temperature ![]() is in the Kelvin scale and the constant of proportionality
is in the Kelvin scale and the constant of proportionality ![]() is Boltzmann’s constant. The value of Boltzmann’s constant is very tiny, in the metric system,
is Boltzmann’s constant. The value of Boltzmann’s constant is very tiny, in the metric system, ![]() .
.
E pluribus unum and the ideal gas
Now we have two macroscopically observable properties, temperature and pressure, that are direct results of the submicroscopic energy and momentum states of all the gas particles we cannot see. As in the motto of the United States, e pluribus unum, “out of many, one,” so with kinetic theory, from many submicroscopic particles, we extract one energy parameter, the temperature, and one momentum parameter, the pressure. This ideal gas model is useful, because a real gas measured in the lab is very close in its properties to the ideal gas model.
Liquid water and the definition of the calorie
One of the metric system definitions of energy is the calorie. It is different from the Joule, but one can use calories wherever one uses Joules. A thermochemical calorie is defined as the amount of energy required to heat up 1.00 gram of liquid water from 14.5°C to 15.5°C, at 1.00 atmosphere of ambient pressure — i.e., at sea level on a fair day. One thermochemical calorie, 1.00 cal, is equivalent to 4.184 Joules. This is different from the conventional food calorie, which customarily uses a capital C and is equivalent to one thousand thermochemical calories: 1000 cal = 1.000 Cal. These big calories appear in nutrition facts on food packaging, such as the Twinkies nutrition fact, 150 calories for one serving. Twinkies notwithstanding, we will do almost all of our thermal calculations in thermochemical calories.
How do you heat up carbon dioxide and other substances?





We mentioned heating up water and carbon dioxide, and we know that temperature changes correspond to changes in the energy state, on average, of the many particles in the sample of water or carbon dioxide. If you fire up your propane burner, you can heat up water, but how much of your propane supply will it take? The amount of heating energy, for which the customary symbol is ![]() , depends on three physical properties of the substance: its mass, how many degrees you want to heat it up, and exactly what kind of substance you have.
, depends on three physical properties of the substance: its mass, how many degrees you want to heat it up, and exactly what kind of substance you have.
- The mass of the substance,
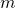 . Your solid substance has interatomic or intermolecular bonding, holding it in crystalline or other rigid arrangement.
. Your solid substance has interatomic or intermolecular bonding, holding it in crystalline or other rigid arrangement. - Temperature change,
 . To heat up the substance, you must change the energy states, 1°C needing half as much energy as heating up by 2°C . Similarly, for cooling, one must extract twice as much energy to cool by -2°C , compared to cooling by only -1°C .
. To heat up the substance, you must change the energy states, 1°C needing half as much energy as heating up by 2°C . Similarly, for cooling, one must extract twice as much energy to cool by -2°C , compared to cooling by only -1°C . - The kind of substance you have. Some substances are easy to heat up, some are not easy to heat up. The easiness or difficulty of heating up, gram for gram and degree for degree, is the specific heat,
 . Liquid water’s specific heat is
. Liquid water’s specific heat is 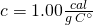 .
.
The formula for computing heating up or cooling down energy Q is just the product of the three physical quantities, viz.
![]()
and the sign of ![]() determines the sign of
determines the sign of ![]() . That is, if you are cooling the substance,
. That is, if you are cooling the substance, ![]() is negative, so
is negative, so ![]() will be negative. Vice versa, if you are heating up the substance,
will be negative. Vice versa, if you are heating up the substance, ![]() is positive, so
is positive, so ![]() will also be positive.
will also be positive.
For the remainder of the chapter, we will keep to the Kelvin scale. It is a metric system scale, but oriented to the kinetic theory, not the behavior of H2O. The Celsius scale goes to zero when water freezes, but the Kelvin scale goes to zero at the theoretical point where molecular kinetic energy is zero.The size of a Kelvin degree, 1.00 K, is the same size as a Celsius degree, 1 C°. The zero point of the Kelvin scale is deep in the negatives of the Celsius scale, -273°C. The freezing point of H2O is 273.15 Celsius-sized degrees above the zero point at T = 0.00 K.
OpenStax.org attribution: Access for free at https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
Note: it is customary to state the units of Kelvin temperature with a capital K but without the ° degree symbol. There are still 100 degrees of separation between H2O freezing and boiling points, but the scales are labeled with different numerals, 0 for Celsius, 273.15 for Kelvin at the freezing point.
Working out a few realistic examples of heating and cooling

“Kaffesugen Kodak” by Thomas Backa is licensed under CC0 1.0


A typical coffee maker heats up tap water to boiling. So let’s work out how many calories of energy it takes to heat up 350 grams of H2O, from tap water temperature 300 K up to boiling point, 373 K. We will use the regular heating formula, ![]() .
.
- mass
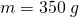 ,
, - specific heat,
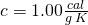 for liquid water,
for liquid water, 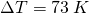
![]()
You can see that the units of grams and Kelvins cancel, but calories remain, which is appropriate. The value of the energy required for this process is ![]() .
.
As a second example, let’s work with solid H2O, ice. Let’s take a 350 g slab of ice out of a commercial freezer that is set to 0°F, or 255 K. We want to heat it up to the melting point, 273 K. But this is solid water, its molecules more organized than the same amount of liquid H2O, so the ice is actually easier to heat up.




In the laboratory, the specific heat of H2O ice measures out at ![]() . That is half as large as the specific heat of liquid water. It means that H2O ice only needs 0.500 calorie to increase the temperature of one gram by one Kelvin. The calculation of energy Q proceeds in a similar manner:
. That is half as large as the specific heat of liquid water. It means that H2O ice only needs 0.500 calorie to increase the temperature of one gram by one Kelvin. The calculation of energy Q proceeds in a similar manner:
![]()
![]()
Our third example will be to heat up a 2.00 kg ingot of aluminum by 607 K. Let’s start at initial temperature 293 K, room temperature, and heat it up to 900 K, slightly below its melting point. At specific heat ![]() , aluminum is relatively easy to heat up, gram for gram and Kelvin for Kelvin. But in this example, we also have a large amount of aluminum,
, aluminum is relatively easy to heat up, gram for gram and Kelvin for Kelvin. But in this example, we also have a large amount of aluminum, ![]() .
.




So even though each gram is relatively easy to heat up by one Kelvin, there are so many grams to heat up that our energy budget for this process, Q, must be quite large:
![]()
This calculates out to a ![]() , and it is not even to the melting point yet!
, and it is not even to the melting point yet!
How to melt ice, aluminum and anything else
Now let’s look at the energy requirements for actually melting solid H2O into liquid H2O, or solid aluminum into liquid aluminum. Once you have heated your substance to the melting point, the intermolecular bonding will begin to degrade. The molecules, on average, have attained an elevated energy state from which their intermolecular bonds are vulnerable, for instance the crystalline bonds of H2O ice or the metallic bonds of aluminum. After crystalline or metallic bonds have broken down, neighboring molecules might still experience weak interactions, as a liquid, strong enough to keep a droplet round and not randomly shaped, but not strong enough to reforge good strong crystalline or metallic bonds. That is, their average kinetic energy is too high to get a pervasive, strong lockdown crystalline bond or metallic bond. A similar logic applies to the vaporization phase transition between a liquid, loosely bonded molecules, to a gas, no bonds of any kind, complete chaos.
But how much energy does it take to degrade the bonds? The degrading goes pair by pair of molecules, so it depends entirely on how many molecules are in your sample. A scientist might measure this in grams or kilograms. And the energy requirements differ for each phase transition, whether you are breaking down a solid or breaking down a liquid. Scientists measure various substance carefully by isolating a liquid and letting it evaporate, or by taking solids and melting them. The amount of energy measured per gram of substance is called the latent heat. In addition, for each substance, there is a latent heat of fusion (melting or freezing) and a latent heat of vaporization (boiling or condensing). Here is a small table of some latent heats.
| Substance | Specific heat, solid |
Specific heat, liquid |
Latent heat of fusion |
Latent heat of vaporization |
| H2O | 0.50 | 1.00 | 80 | 539 |
| Ethanol | 0.58 | 0.58 | 25.8 | 214 |
| Copper | 0.386 | 0.118 | 49 | 1128 |
| Gold | 0.126 | 0.036 | 15 | 400 |
| Lead | 0.128 | 0.033 | 5.5 | 205 |

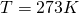 .
. “135/365: cool” by Mark Bonica is licensed under CC BY 2.0


Notice how much easier lead is to melt, compared to H2O ice, gram for gram. Gold is also relatively easy to melt.
One of the interesting properties of matter is connected to latent heat. That is, when you heat up a sample, its temperature increases until it gets to the melting point, but then it is stuck at the melting point as you continue to pour on the calories. The process of melting takes over, so each calorie breaks apart the solid into its liquid state. Once all of the solid is melted, then the liquid’s temperature begins to rise. Ice water is an example of this. Theoretically, you can use a beaker of ice water to keep a test tube of any substance at 273 K, as long as the ice remains. If your ice water container is fairly well insulated, this could last for quite a while.
Heat transport
There are three ways heat energy flows from point A to point B: conduction, convection and radiation. There is only one condition for heat to flow from point A to point B: if the temperatures are different at each point. To determine if two quantities of matter are in thermal equilibrium, one must look at the two temperatures.
- If the two temperatures are equal, they are in thermal equilibrium.
- If the two temperatures are unequal, one will be larger, the other smaller, and heat energy will flow from the larger temperature substance to the lower temperature substance.
Conduction
Two good example of this condition, unequal temperature, are well-known to doctors and nurses in the emergency room:
- A swimmer in the ocean, without a wetsuit, can develop hypothermia very rapidly, and the emergency room will place warm compresses on the swimmers neck, chest and lower abdomen, to warm up the body core. Advanced treatment includes blood rewarming, with the patient’s blood circulating through a dialysis machine or similar device. These treatments cause heat energy to flow from external hot objects or rewarmed blood into the colder body core.
- Against this example, you may also consider a case of heat stroke. One of the emergency treatments for heat stroke is immersion in a bath of ice water! In this case, heat flows from the patients body into the bath of ice water.
In both of the examples, hypothermia and heat stroke, the direction of heat energy is from higher temperature to lower temperature, and the transport mode is conduction. That is, the hot compresses, the rewarmed blood, the heat stroke patient, are actually in contact with the colder substance, and heat energy diffuses across the boundary between the two. In the emergency room, the doctors and nurses monitor the patient’s temperature carefully. They do not want any random equilibrium temperature: they want the patient to force the patient’s temperature to 98.6°F, 37°C, 310 K. Then, as they trust and hope, the patient’s normal biological function maintains stable body temperature.
In a laboratory, you might allow two gases to interact and reach their own equilibrium temperature, without forcing. For example, you could take a warm gas at initial temperature 500 K, in an insulated container, and another gas at initial temperature 400 K, in an insulated container.
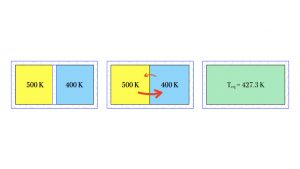
If you remove the insulating wall separating the two samples, the gases begin to mix and equilibrate. The average kinetic energy of the molecules of warmer gas move into the cooler region more rapidly than the poky molecules in the cooler gas, which have lower average kinetic energy. It is true that the poky molecules from the cooler gas do spread to the warmer region, but they do not do so very rapidly, due to pokiness — i.e., due to lower average kinetic energy. The diagram above shows this in the two red arrows: larger and thicker for the blazing average kinetic energy of the molecules of the warmer gas, and a smaller, thinner arrow for the poky average kinetic energy of the cooler gas. So, thinking in terms of kinetic energies, more net kinetic energy crosses from the warm side to the cool side. The hot side might still read a relatively higher temperature, but its average kinetic energy is decreasing due to a higher number of poky molecules, so its temperature might dip to 499 K in the first second of mixing. Similarly, the cool side is hotting up, due to the arrival of molecules with high average kinetic energy, and its temperature might blaze upward to 400.3 K in that same first second of interaction.
Eventually, the molecules of each gas mix so thoroughly that the entire sample of the mixture has arrived at one temperature, the equilibrium temperature. In the diagram above, the equilibrium temperature is 427.3 K. Is it plausible that the equilibrium temperature is not exactly halfway between the two initial temperatures? Yes, it might be off center, because the two gases
- might be different gases, which might mean different specific heats, and
- might be different amounts, more grams of the cooler gas, for instance, and
- in their separate containers, their initial pressures, which we did not mention, might also have been different.
Even if everything is different — different specific heats, different amounts, different pressures — they will attain an equilibrium temperature somewhere below the hotter gas’ initial temperature and above the cooler gas’ initial temperature.
Convection





Convection is a heat transport method that tends to proceed in a fluid that is not a very good conductor of heat. Instead of conducting, a bolus of warm material rises through cooler material, without losing much energy by conduction. This transports heat energy. An example is a fire breather. He spews liquid paraffin out and up, and ignites it (by conduction!) with a small side torch. Instead of arcing across a parabolic path, however, the mass of ignited paraffin heats up the air and the entire fireball lifts upward. The mass of high temperature fuel-air mixture moves from point A upward to point B. This only works with cooler surrounding air, which is more dense. The ignited fuel-air mixture is at a lower density, and buoyant forces give it some upwards F = ma force.
A similar example of hot air rising, cool air descending is a hot air balloon. They work best when the surrounding air is cool, in the early morning. The buoyancy force on the hot air in the balloons lofts the entire balloon.




But once aloft, they can stay aloft by periodically burning their propane upward into the balloon. If they need to descent back to terra firma, they just vent the balloon, less hot air, left buoyancy force, net force downward.
All of this works because air is a poor conductor of heat, or, as we might say, it is a good insulator. You can understand this by looking at a fleece vest or a fur hat or soft nice winter gloves or a thick, comfy scarf. The fibers have many small air spaces between them, trapping air, a good insulator. Being trapped, the air cannot convect and move warm air toward cooler air, keeping you warm and comfy. Some fibers actually contain tiny air pockets, further increasing the insulating power. Alpacas might be funny looking, but do not make fun of them, because their hair is hollow, keeping them warm and happy at the high altitudes of the Peruvian Andes.





Humans have also figured out how to manufacture hollow polyester fibers, too. Many trademarked names reflect this, such as Hollofil®, a synthetic polyester popular with bedding and pillows. Backpackers use another hollow core fiber, Polarguard® Delta, for very lightweight sleeping bags and parkas. These fibers keep in warmth and are not rendered useless by getting soaked with water. Goose down is the best insulator for very cold conditions. However, goose down has to stay dry, because it tends to hold onto water, and water is a relatively good conductor of heat.
Radiation
The concept of radiation as a heat transport method, is based on what we know about light. Each photon of light carries energy and momentum.
- A substance that absorbs the photon’s energy and momentum will tend to heat up.
- A substance that is transparent to light, does not absorb much energy and does not heat up very much at all.
Our planet is warm because of radiative heat transport from the photosphere of the Sun, the outermost layer of the Sun from which most visible light is emitted.




But interplanetary space is quite happy to grant photons a free passage, so most of the light aimed toward Earth actually does arrive here. It warms the oceans and the atmosphere and all of the water vapor in the atmosphere. Most of our weather depends on solar radiation. Anyone living in Florida knows that the surface temperature has a dramatic effect on the intensity of hurricanes.
Examples
Example 1. Forty grams of H2O ice





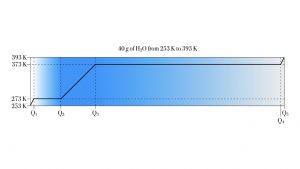
A 40 g sample of H2O ice at initial temperature 253 K must be converted to steam at final temperature 393 K.
What is the energy budget, total energy required, for this process?
SOLUTION:
This heat-melt-heat-boil-heat process takes the 40 grams of H2O through both phase transitions. It also heats the H2O in each phase. In list form, it is
- heat the ice up to 273 K, the melting point;
- melt all 40 grams of ice at 273 K;
- heat the liquid H2O from 273 K up to the boiling point, 373 K;
- boil the 40 g of H2O to form 40 g of steam at 373;
- heat up the steam to the target temperature of 393 K.
We have five ![]() calculations to work out. The following diagram shows the five stages of heating.
calculations to work out. The following diagram shows the five stages of heating.
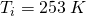 all the way to steam at
all the way to steam at 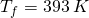 .
.Let’s work out each part of the energy budget, stage by stage.
- First, we heat the ice, each gram of which heats up 1.0 K for every 0.50 cal of heat added. I.e., the specific heat of H2O ice is 0.50 cal/g K. Our formula for this stage is
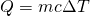 .
.
![Rendered by QuickLaTeX.com \[Q_1=mc\Delta T=\left(40\: g\right)\left(0.50\frac{cal}{g\: K}\right)\left(273\: K-253\: K\right)\longrightarrow Q_1=400\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-7b712e072cc792f7a63f6f5d799c8f07_l3.png)
- Next, we melt all of it. This requires 80 calories for each gram. I.e., the latent heat of fusion for H2O is
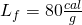 .
.
![Rendered by QuickLaTeX.com \[Q_2=\left(40\: g\right)\left(80\frac{cal}{g}\right)=3200\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-39164d165e689e387a2554147e41bf7b_l3.png)
![Rendered by QuickLaTeX.com \[\text{total }Q=3600\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-143f053b812e23d6c1ffcb912a7a451d_l3.png)
- Now it is all liquid water at 273 K, so we heat it up according to its specific heat, the standard value
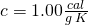 for liquid water. Again, we employ
for liquid water. Again, we employ 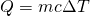 .
.
![Rendered by QuickLaTeX.com \[Q_3=mc\Delta T=\left(40\: g\right)\left(1.00\frac{cal}{g\: K}\right)\left(373\: K-273\: K\right)\longrightarrow Q_3=4000\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-cb381f0f7c9345010b8e9bf93aeea80f_l3.png)
![Rendered by QuickLaTeX.com \[\text{total }Q=7600\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-4753e514827e0767e0580db5b5073bbd_l3.png)
- Here is the big energy stage. We have to boil the water until it all turns to steam. The latent heat of vaporization is quite large,
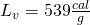
![Rendered by QuickLaTeX.com \[Q_4=\left(40\: g\right)\left(539\frac{cal}{g}\right)=21560\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-8a2eb96612e673bffc582986f192ffa4_l3.png)
![Rendered by QuickLaTeX.com \[\text{total }Q=29160\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-dc14957f3d840171f2371e9bf86dfa90_l3.png)
- Last stage is just heating up the steam another 20 K. This is the final application of the heat-up equation,
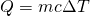 . The specific heat of water vapor in the lab is approximately 0.45 cal/g K.
. The specific heat of water vapor in the lab is approximately 0.45 cal/g K.
![Rendered by QuickLaTeX.com \[Q_5=mc\Delta T=\left(40\: g\right)\left(0.45\frac{cal}{g\: K}\right)\left(393\: K-373\: K\right)\longrightarrow Q_5=360\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-7d9bebf1b18c30c99b5d6d8b36d37473_l3.png)
![Rendered by QuickLaTeX.com \[\text{total }Q=29520\: cal\]](https://pressbooks.online.ucf.edu/app/uploads/quicklatex/quicklatex.com-468e01c89ce312f74aac92a2df157142_l3.png)
So the total energy budget is ![]() for this process.
for this process.
Example 2. Finding an equilibrium temperature for a mixture of fluids.
In a well insulated container, you mix 20 grams of liquid water, initially at temperature 290.00 K, with a 40 gram squirt of ethanol, initially at a colder temperature, 275.00 K.
Find the equilibrium temperature.
SOLUTION:
In this process, the liquid ethanol will absorb energy from the water. Since the container is insulated, the ethanol is the only thing that can absorb energy from the water. This is actually another example of the conservation of total energy, this time including the heat energy. Therefore the ethanol’s equilibrium temperature will be above 275 K. Also, every calorie of energy that the water loses also serves to decrease its temperature. Therefore the equilibrium temperature will be below 290 K. The water cools down, energy flows into the ethanol, and the ethanol warms up. Calorie by calorie, the temperatures change, getting closer for each calorie exchanged.
For instance, when the water surrenders 10 calories, ![]() , then the ethanol absorbs 10 calories,
, then the ethanol absorbs 10 calories, ![]() . Each changes temperature as a result. We can calculate those two
. Each changes temperature as a result. We can calculate those two ![]() ‘s: for the water,
‘s: for the water, ![]() , and for the ethanol,
, and for the ethanol, ![]() .
.
| Water
|
Ethanol
|
One can see in this that the ethanol just a bit harder to heat up, calorie for calorie, than the water is to cool down. That is, after exchanging 10 calories, the water cools a bit more than the ethanol heats up.
When the two fluids exchange 10 calories, the temperatures change to 289.50 K for water and 275.43 K for the ethanol. This is level 1 in the sequence. After another exchange of 10 calories, sequence level 2, the water is down to 289.00 K and ethanol is up to 275.86 K. They are closer, but still not at equilibrium. Nature continues to exchange calories of energy, inching closer to equilibrium.
|
Sequence |
Water temperature (K) |
Q exchange (calories) |
|
|
|
0 |
290.00 |
|
|
|
|
1 |
289.50 |
-10 |
|
|
|
2 |
289.00 |
-10 |
|
|
|
3 |
288.50 |
-10 |
|
|
|
4 |
288.00 |
-10 |
|
|
|
5 |
287.50 |
-10 |
|
|
|
6 |
287.00 |
-10 |
|
|
|
7 |
286.50 |
-10 |
|
|
|
8 |
286.00 |
-10 |
|
|
|
9 |
285.50 |
-10 |
|
|
|
10 |
285.00 |
-10 |
|
|
|
11 |
284.50 |
-10 |
|
|
|
12 |
284.00 |
-10 |
|
|
|
13 |
283.50 |
-10 |
|
|
|
14 |
283.00 |
-10 |
|
|
|
15 |
282.50 |
-10 |
|
|
|
16 |
282.00 |
-10 |
|
|
|
|
|
✔︎ |
|
|
|
|
|
10 |
281.88 |
16 |
|
|
|
10 |
281.45 |
15 |
|
|
|
10 |
281.02 |
14 |
|
|
|
10 |
280.58 |
13 |
|
|
|
10 |
280.16 |
12 |
|
|
|
10 |
279.73 |
11 |
|
|
|
10 |
279.30 |
10 |
|
|
|
10 |
278.87 |
9 |
|
|
|
10 |
278.44 |
8 |
|
|
|
10 |
278.01 |
7 |
|
|
|
10 |
277.58 |
6 |
|
|
|
10 |
277.15 |
5 |
|
|
|
10 |
276.72 |
4 |
|
|
|
10 |
276.29 |
3 |
|
|
|
10 |
275.86 |
2 |
|
|
|
10 |
275.43 |
1 |
|
|
|
|
275.00 |
0 |
|
|
|
Q exchange (calories) |
Ethanol temperature (K) |
Sequence |
After about 160 calories have flowed out of the water and into the ethanol, their temperatures are both fairly close to 282 K. Therefore, the equilibrium temperature is approximately 282 K.
If you had tried a hypothetical exchange of heat energy ![]() , then each temperature step would be smaller. You would need about 32 steps in your sequence of temperatures, and a longer table, to figure out the equilibrium temperature. This would be helpful, because you might get a bit more precision on the equilibrium temperature, because level 32 temperatures would be closer than 282 K and 281.88 K in the table above.
, then each temperature step would be smaller. You would need about 32 steps in your sequence of temperatures, and a longer table, to figure out the equilibrium temperature. This would be helpful, because you might get a bit more precision on the equilibrium temperature, because level 32 temperatures would be closer than 282 K and 281.88 K in the table above.
Alternatively, you had tried a hypothetical exchange of heat energy ![]() , then each temperature step would be larger. That would lead to a smaller table, a faster calculation, about eight levels in the sequence, but less precision as to the actual equilibrium temperature.
, then each temperature step would be larger. That would lead to a smaller table, a faster calculation, about eight levels in the sequence, but less precision as to the actual equilibrium temperature.
Note: This is an idealized mixing problem. Real ethanol and water dissolve, and the process of these two compounds dissolving actually gives off energy as heat.
Comments
The sequence parameter in the table above is a one-way parameter for both substances. That is, nature does not run in the opposite direction, from cool ethanol to even cooler ethanol and warm water to even warmer water. Nature does not proceed in the manner of energy flowing out of a cool object and into a hot object, if one looks at average temperatures. Nature never does this. It only proceeds by way of energy flowing from a hot object into a cooler object, from a hot collection of particles into a cold collection of particles. This makes the sequence parameter like time itself.
As mathematical physicist John Baez once wrote, “Why is the future so much different from the past?”[1] He noted that we make plans for a time in the future; nobody plans for something that happened last Tuesday. Similarly, we remember past events only; one does not simply remember things that happen next Thursday. We are on a one-way trip into the future, at the speed of 60 minutes per hour, just as the thermal behavior of the water and alcohol is on a one-way trip to thermal equilibrium. This comparison of thermal behavior to our sense of time is called the thermodynamic arrow of time. Neither John Baez nor Albert Einstein nor anyone else has ever explained this scientifically. Time is the deepest riddle of them all.
- Baez, John. "Open Questions in Physics." Last modified: September 21, 2007. http://www.math.ucr.edu/home/baez/open.questions.html ↵
