Work [W]

Work is not a property, but the transmission of energy by force. Again, the most fundamental expression for work is as follows

$$\int_{{s_1}}^{s_{2}} {\bf F} \cdot d{\bf s}.$$

This expression allows the magnitude of force to change along its path of action s, as a process proceeds from state (1) to a final state (2). The high school physics definition of work, “force times distance” must be broadened to incorporate forms of work relevant to thermodynamics. The thermodynamic definition of work: Work is done by a system on its surroundings if the outcome could have been the raising of a weight. Think of it his way, if work to compress a spring, I’ve done work to my surroundings. The energy now stored in the spring could be used to raise a weight as the spring uncoils.

In this course we consider three modes of work transfer across the boundary of a system, as shown in the following diagram:

Three forms of Work considered:
a) Boundary Work [latex]W_b \implies[/latex] Piston – Cylinder
b) Shaft Work [latex]W_s \implies[/latex] Paddle Wheel
c) Electrical Work [latex]W_e =[/latex]Volts [latex]\cdot I[/latex] (Amps) [latex]\cdot[/latex] time

We are primarily concerned with Boundary Work due to compression or expansion of a system in a piston-cylinder device as shown above. In all cases we assume a perfect seal (no mass flow in or out of the system), no loss due to friction, and quasi-equilibrium processes in that for each incremental movement of the piston equilibrium conditions are maintained. By convention:

$$W>0: \quad \text{work done by the system}$$

$$W<0: \quad \text{work done on the system}$$ This sign convention will be used throughout the course.

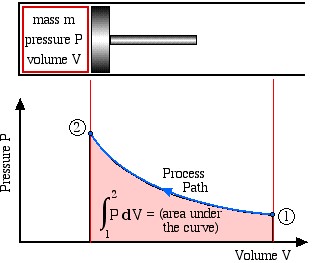
Boundary work is evaluated by integrating the force F multiplied by the incremental distance moved [latex]dx[/latex] between an initial state (1) to a final state (2). Now that we’ve constrained our boundary to move linearly, we can replace [latex]d{\bf s}[/latex] with [latex]dx[/latex]. We normally deal with a piston-cylinder device, thus the force can be replaced by the piston area A multiplied by the pressure P, allowing us to replace [latex]Adx[/latex] by the change in volume dV, as follows:

$$W_{1-2}=\int_1^2F\:dx=\int_1^2PA\:dx=\int_1^2P\:dV,$$

where [latex]\int_{V_{1}}^{V_{2}}dV=V_{2}-V_{1}[/latex]. This is shown in the following schematic diagram, where we recall that integration can be represented by the area under the curve.

[latex]\displaystyle \int_1^2 P\:dV =[/latex] (area under the curve)

Note that work done is a Path Function and not a property, thus it is dependent on the process path between the initial and final states. Sometimes these paths are simplified when one property is held constant. Terms for these special types of paths are as follows:

• Isothermal (constant temperature process)
• Isochoric or Isometric (constant volume process)
• Isobaric (constant pressure process)
• Adiabatic (no heat flow to or from the system during the process)

It is sometimes convenient to evaluate the specific work done which can be represented by a P-v diagram thus if the mass of the system is m [kg] we have finally:

$$W_{1-2}=\int_1^2P\:dV=m\int_1^2P\:dv=m*w_{1-2},$$

where: P is pressure [kPa], V is volume [m³].

m is mass [kg], v is specific volume [latex]\left[\frac{m^3}{kg}\right][/latex].

W is work done [kJ], w is specific work done [latex]\left[\frac{kJ}{kg}\right][/latex].

For an isobaric process, or when pressure is constant, the above integral for boundary work simplifies to

$$W_{1-2}=p\left (V_{2}-V_{1} \right).$$

Again, according to the convention established above, work done by the system on the surroundings (expansion process) is positive, and that done on the system by the surroundings (compression process) is negative. Shaft Work (due to a paddle wheel) likewise carries this convention, but there is no expression, like that for boundary work, that can be used to quantify shaft work.

Power [latex][\dot{W}][/latex]

Engineering analysis often requires the use of time rates of energy delivery. Power ([latex]\dot{W}[/latex]) is the term used to describe the time rate of energy transfer by work. Power may be expressed as the scalar product of force and velocity vectors,

$$\dot{W}={\bf F}\cdot {\bf V}.$$

This equations works nicely for a linearly translating piston, or a car overcoming air drag at a constant speed. In many cases in this course, however, power transmitted by a shaft will be a quantity into a pump, or the output of a turbine. If we know the torque on the shaft [latex]\tau[/latex] and its rotation rate [latex]\omega[/latex],

$$\dot{W}=\tau \omega.$$

But this is rarely the case in high-level thermodynamic analysis. Thus, we will not determine it directly, but use an energy balance (coming in a later node) to calculate power.