Energy Balance for Cycles
A thermodynamic cycle is a series of processes that begin and end at the same thermodynamic state. The figure below demonstrates what a cycle may look like on P-V coordinates.
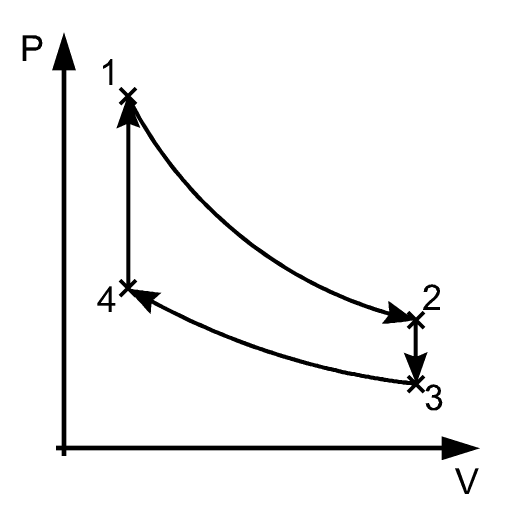
At the end of a cycle, all of the properties of a substance or object (temperature, pressure, specific volume, enthalpy, etc.) have the same value as when the cycle began. Cycles can run just once, a number of times, or continuously. In any case, there is no net change in energy for the cycle. Accordingly,
[latex]\Delta E_\text{cycle} = 0.[/latex]
Remember that for a process or series of processes that [latex]\Delta E = Q-W[/latex] must be satisfied. This is the First Law of Thermodynamics. Written for a cycle, [latex]\cancel{\Delta E_\text{cycle}}=Q_\text{cycle}-W_\text{cycle}[/latex]. So for any cycle,
[latex]Q_\text{cycle}=W_\text{cycle}[/latex].
If we for now suspend the sign convention for [latex]Q[/latex] and [latex]W[/latex], and let absolute values of [latex]W\text{cycle}[/latex], [latex]Q_\text{in}[/latex], and [latex]Q_\text{out}[/latex] denote the work/heat transfer into and out of the system, we may write,
[latex]W_\text{cycle}= Q_\text{in} -Q_\text{out}.[/latex]
This is a convenient expression for use in power and refrigeration cycles, which will be discussed briefly below. It is not critical to remember the above expression verbatim, as it pops out easily from the First Law (which should absolutely be devoted to memory).
Power Cycles

The purpose of a power cycle is to convert heat energy into work, or power if operating on a continual basis. Consider the diagram below. Energy naturally flows from hotter to colder bodies. We can take advantage of this flow by inserting a system into the flow to extract work. This is analogous to a waterwheel. Falling water will descend with or without the wheel present, but we can convert some of the water’s potential energy into shaft work, thereby reducing the kinetic energy it has at the bottom of the fall.
If instead we replace the water with bodies at contrasting temperatures and the waterwheel with a heat engine, we have a generic thermodynamic power cycle. A steam engine is one such real-world example. The magnitude of the work out through one revolution of the cycle is the difference between the heat transfer in and the heat transfer out during that revolution. For a power cycle [latex]W_\text{cycle}[/latex] will always be a positive value.
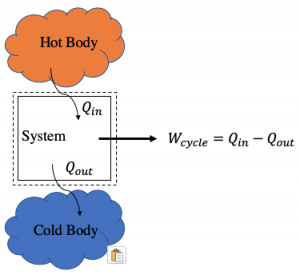
As a simple example, we transfer into a system executing a cycle 10 kJ of heat and 3 kJ of heat leaves the system,
[latex]W_\text{cycle}= Q_\text{in} -Q_\text{out}=10~\text{kJ}-3~\text{kJ}=7~\text{kJ} \quad \text{(power cycle)}[/latex]
The performance of a power cycle, or how well it does converting heat to work, is measured by the thermal efficiency [latex]\eta[/latex]. In words, the thermal is the ratio of “what you want/what you give.”
[latex]\eta = \frac{W_\text{cycle}}{Q_\text{in}}[/latex]
Thermal efficiency can never be negative or greater than 1. Using our definition of [latex]W_\text{cycle}[/latex], we may write thermal efficiency a different way,
[latex]\eta = \frac{Q_\text{in} -Q_\text{out}}{Q_\text{in}}=1-\frac{Q_\text{out}}{Q_\text{in}}.[/latex]
Note that [latex]Q_\text{in} \ge Q_\text{out}[/latex]. Using the numbers given above, that hypothetical cycle would have an efficiency [latex]\eta = W_\text{cycle}/Q_\text{in} = 7~\text{kJ}/10~\text{kJ} = 0.7 = 70\%[/latex]. That’s actually quite good!
Refrigeration/Heat Pump Cycles
Often we want to move heat from a colder to a hotter body. This is what your home/car AC and refrigerators do everyday. Because we are forcing heat to flow in a direction that is “unnatural,” this process requires work input. Therefore, for these type cycles,
[latex]W_\text{cycle}= Q_\text{out} -Q_\text{in}\quad \text{(refrigeration/heat pump cycle)}.[/latex]
This will tell me how much work if must provide to achieve the desired heat transfer.
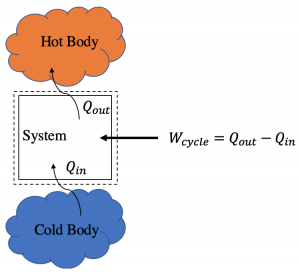
Refrigeration and heat pump cycles operate the same way but have different goals. A refrigeration cycle makes a cold body (or space) colder. A heat pump cycle makes a hot body (or space) hotter. Heat pumps are commonly used to heat homes by running your home AC in reverse.
We can only define a thermal efficiency for power cycles. But, we still need a measure of how effective a refrigeration/heat pump cycle is at using work to produce heat transfer. For this we will still employ the “what you want/what you give” principle to define a coefficient of performance (COP).
For refrigeration cycles the COP is
[latex]\beta = \frac{Q_\text{in}}{W_\text{cycle}}=\frac{Q_\text{in}}{Q_\text{out} -Q_\text{in}},[/latex]
where both inputs must be provided as absolute values (ignoring previously established sign conventions). For heat pump cycles the COP is
[latex]\gamma = \frac{Q_\text{out}}{W_\text{cycle}}=\frac{Q\text{out}}{Q_\text{out} -Q_\text{in}},[/latex]
where both inputs must be provided as absolute values (ignoring previously established sign conventions). Note that ALL of the work input to these cycles is converted to heat. For heat pump cycles, this is advantageous as that conversion to heat helps accomplish the cycle’s goal.

