Internal energy (U) of a body is that associated with the molecular activity of the body as indicated by its temperature T [°C], and can be evaluated in terms of the heat required to change the temperature of the body having a specific heat capacity [latex]C\left[\frac{J}{kg\times°C}\right][/latex], as follows:

$$Q=m\times C\times\Delta T=m\times\Delta u=\Delta U.$$

Internal energy is an extensive property. By thinking of the molecules which comprise a body or substance, we can visualize increases in internal energy by increases in molecular motion, and thus temperature. Therefore, it should be obvious why the stirring of a fluid by a paddle wheel (shaft work) creates an increase in a system’s internal energy (and temperature by extension).

Total Energy

The total energy E of a system is simply the sum of its internal, kinetic, an potential energies:

$$E = me = m(u+ke+pe)=U+KE+PE.$$

Likewise the change of the total energy of a system is the sum of the changes in the respective energies:

$$\Delta E = m\Delta e = m(\Delta u+\Delta ke+\Delta pe)=\Delta U+\Delta KE+\Delta PE$$

$$E_{2}-E_{1}= \left (U_{2}- U_{1}\right )+\left (KE_{2}- KE_{1}\right )+\left (PE_{2}- PE_{1}\right )$$

Example: Cooking with Potential Energy

In order to gain an intuitive appreciation for the relative magnitudes of the different forms of energy we consider the (tongue-in-cheek) example of an attempt to cook a turkey by potential energy. The turkey is brought to the top of a 100 m building (about 30 stories) and then dropped from the ledge. The potential energy is thus converted into kinetic energy, and finally on impact the kinetic energy is converted into internal energy. The increase in internal energy is represented by an increase in temperature, and hopefully, if this experiment is repeated enough times the temperature increase will allow the turkey to cook. This remarkable experiment was first reported by R.C.Gimmi and Gloria J Browne – “Cooking with Potential Energy“, published in the Journal of Irreproducible Results (Vol. 33, 1987, pp 21-22).

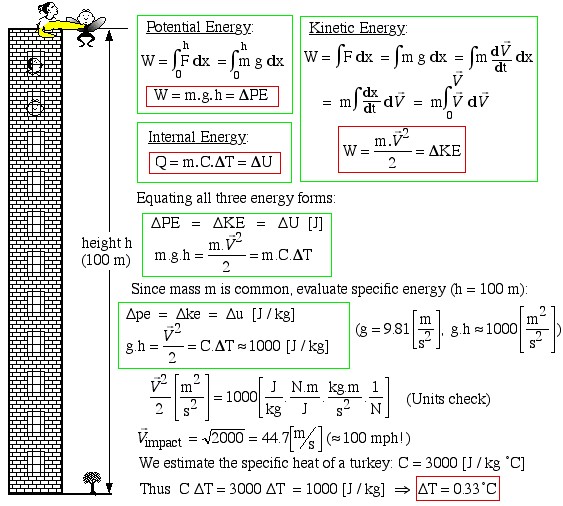
Potential Energy

[latex]W=\int_0^h F \ \mathrm{d}x = \int_0^h m g \ \mathrm{d}x[/latex]

[latex]\color{red}\boxed{\color{black}W=m\cdot g \cdot h=\Delta PE}[/latex]

Internal Energy

[latex]\color{red}\boxed{\color{black}Q=m \cdot C \cdot \Delta T = \Delta U}[/latex]

\begin{align*}
W &= \int F \ \mathrm{d}x = \int mg \ \mathrm{d}x = \int m \frac{\mathrm{d}\vec{V}}{\mathrm{d}t} \ \mathrm{d}x \\
&= m \int \frac{\mathrm{d}x}{\mathrm{d}t} \ \mathrm{d}\vec{V} = m \int_0^{\vec{V}} \vec{V} \ \mathrm{d}\vec{V}
\end{align*}
$$\color{red}\boxed{\color{black}W=\frac{m \cdot \vec{V}^2}{2}=\Delta KE}$$

Equating all three energy forms:
[latex]\Delta PE = \Delta KE = \Delta U \ [\text{J}][/latex]

[latex]m \cdot g \cdot h=\frac{m \cdot \vec{V}^2}{2} = m \cdot C \cdot \Delta T[/latex]

Since mass m is common, evaluate specific energy (h=100 m):
[latex]\Delta pe = \Delta ke = \Delta u \ [\text{J/kg}][/latex]

[latex]g \cdot h = \frac{\vec{V}^2}{2} = C \cdot \Delta T \approx 1000 \ [\text{J/kg}][/latex]

[latex]\frac{\vec{V}^2}{2} \left[\frac{\text m^2}{\text s^2}\right] = 1000 \left[ \frac{\text J}{\text kg} \cdot \frac{\text{ N m}}{\text J} \cdot \frac{\text{ kg m}}{\text{ s}^2} \cdot \frac{1}{\text N}\right][/latex]

[latex]\vec{V}_{\text{impact}} = \sqrt{2000} = 44.7 \ [\text{m/s}] (\approx 100 \ \text{mph}!)[/latex]

We estimate the specific heat of a turkey.
[latex]C = 3000 \ [\text{J/kg}{^{\circ}C}][/latex]

Thus
[latex]C \Delta T = 3000 \ \Delta T = 1000 \ [\text{J/kg}] \implies \color{red}\boxed{\color{black} \Delta T = 0.33 ^{\circ}C}[/latex]

What a disappointment! At 0.33°C per fall it will require repeating the experiment 600 times just to reach the cooking temperature of 200°C.