Energy Balance for Closed Systems

Now that you have learned how to calculate the various forms of energy, kinetic, potential, and internal, and know how energy is transferred via heat and work, it’s time to put all of it together. The First Law of Thermodynamics applied to stationary closed systems as a conservation of energy principle. For a closed system (no mass transfer) process proceeding between two states:

$$\Delta E = \Delta  KE+\Delta  PE+\Delta U=Q-W.$$

This is one to commit to memory! Energy is transferred between the system and the surroundings in the form of heat and work, resulting in a change of total energy of the system. When using this equation, do not forget the sign conventions for heat and work we learned earlier.

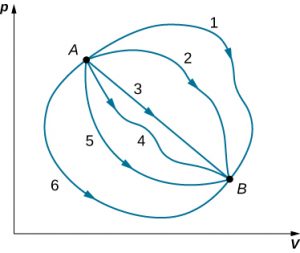
Although Q and W both depend on the thermodynamic path taken between two equilibrium states, their difference <emQ−W does not.  The figure below shows the pV diagram of a system that is making the transition from A to B repeatedly along different thermodynamic paths. Along path 1, the system absorbs heat Q₁ and does work W₁; along path 2, it absorbs heat Q₂ and does work W₂, and so on. The values of Q_i and W_i may vary from path to path, but we have

That is, the change in the internal energy of the system between A and B is path independent. In the chapter on potential energy and the conservation of energy, we encountered another path-independent quantity: the change in potential energy between two arbitrary points in space. This change represents the negative of the work done by a conservative force between the two points. The potential energy is a function of spatial coordinates, whereas the internal energy is a function of thermodynamic variables. For example, we might write [latex]U(T,p)[/latex] for the internal energy. Functions such as internal energy and potential energy are known as state functions because their values depend solely on the state of the system.

Often the first law is used in its differential form, which is

$$dE=dQ−dW.$$

Here dE is an infinitesimal change in total energy when an infinitesimal amount of heat dQ is exchanged with the system and an infinitesimal amount of work dW is done by (positive in sign) or on (negative in sign) the system.

The time rate of change of energy within a system is expressed

$$\frac{dE}{dt}=\dot{Q}-\dot{W}.$$

In words this equation is: [the time rate of change of energy in a system at time t] = [the net rate of heat transfer into a system at time t] – [the net rate of work out of a system at time t]. Notice the quantities with dots above them represent rates at a moment in time. In this course we will almost always treat these rates of transfer as invariant in time. If we expand the above equation to include the three forms of energy of interest,

$$\frac{dE}{dt}=\frac{KE}{dt}+\frac{PE}{dt}+\frac{dU}{dt}=\dot{Q}-\dot{W}$$

Quite often kinetic and potential energies do not vary in time (for systems which are stationary, for example). In this case, we are left with

$$\frac{dU}{dt}=\dot{Q}-\dot{W}.$$