Chapter 15 The Sun: A Garden-Variety Star
15.7 Questions and Exercises
Review Questions
1: Describe the main differences between the composition of Earth and that of the Sun.
2: Describe how energy makes its way from the nuclear core of the Sun to the atmosphere. Include the name of each layer and how energy moves through the layer.
3: Make a sketch of the Sun’s atmosphere showing the locations of the photosphere, chromosphere, and corona. What is the approximate temperature of each of these regions?
4: Why do sunspots look dark?
5: Which aspects of the Sun’s activity cycle have a period of about 11 years? Which vary during intervals of about 22 years?
6: Summarize the evidence indicating that over several hundreds of years or more there have been variations in the level of the solar activity.
7: What it the Zeeman effect and what does it tell us about the Sun?
8: Explain how the theory of the Sun’s dynamo results in an average 22-year solar activity cycle. Include the location and mechanism for the dynamo.
9: Compare and contrast the four different types of solar activity above the photosphere.
10: What are the two sources of particles coming from the Sun that cause space weather? How are they different?
11: How does activity on the Sun affect human technology on Earth and in the rest of the solar system?
12: How does activity on the Sun affect natural phenomena on Earth?
Thought Questions
13: Table 15.1 indicates that the density of the Sun is 1.41 g/cm3. Since other materials, such as ice, have similar densities, how do you know that the Sun is not made of ice?
14: Starting from the core of the Sun and going outward, the temperature decreases. Yet, above the photosphere, the temperature increases. How can this be?
15: Since the rotation period of the Sun can be determined by observing the apparent motions of sunspots, a correction must be made for the orbital motion of Earth. Explain what the correction is and how it arises. Making some sketches may help answer this question.
16: Suppose an (extremely hypothetical) elongated sunspot forms that extends from a latitude of 30° to a latitude of 40° along a fixed of longitude on the Sun. How will the appearance of that sunspot change as the Sun rotates? (Figure 15.17 should help you figure this out.)
17: The text explains that plages are found near sunspots, but Figure 15.18 shows that they appear even in areas without sunspots. What might be the explanation for this?
18: Why would a flare be observed in visible light, when they are so much brighter in X-ray and ultraviolet light?
19: How can the prominences, which are so big and ‘float’ in the corona, stay gravitationally attached to the Sun while flares can escape?
20: If you were concerned about space weather and wanted to avoid it, where would be the safest place on Earth for you to live?
21: Suppose you live in northern Canada and an extremely strong flare is reported on the Sun. What precautions might you take? What might be a positive result?
Figuring for Yourself
22: The edge of the Sun doesn’t have to be absolutely sharp in order to look that way to us. It just has to go from being transparent to being completely opaque in a distance that is smaller than your eye can resolve. Remember from Astronomical Instruments that the ability to resolve detail depends on the size of the telescope’s aperture. The pupil of your eye is very small relative to the size of a telescope and therefore is very limited in the amount of detail you can see. In fact, your eye cannot see details that are smaller than 1/30 of the diameter of the Sun (about 1 arcminute). Nearly all the light from the Sun emerges from a layer that is only about 400 km thick. What fraction is this of the diameter of the Sun? How does this compare with the ability of the human eye to resolve detail? Suppose we could see light emerging directly from a layer that was 300,000 km thick. Would the Sun appear to have a sharp edge?
23: Show that the statement that 92% of the Sun’s atoms are hydrogen is consistent with the statement that 73% of the Sun’s mass is made up of hydrogen, as found in Table 15.2. (Hint: Make the simplifying assumption, which is nearly correct, that the Sun is made up entirely of hydrogen and helium.)
24: From Doppler shifts of the spectral lines in the light coming from the east and west edges of the Sun, astronomers find that the radial velocities of the two edges differ by about 4 km/s, meaning that the Sun’s rotation rate is 2 km/s. Find the approximate period of rotation of the Sun in days. The circumference of a sphere is given by 2πR, where R is the radius of the sphere.
25: Assuming an average sunspot cycle of 11 years, how many revolutions does the equator of the Sun make during that one cycle? Do higher latitudes make more or fewer revolutions compared to the equator?
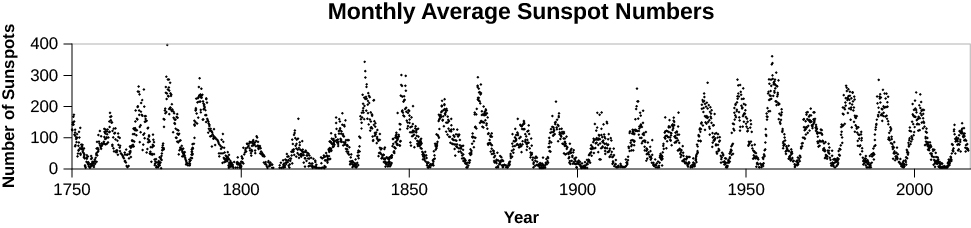
26: This chapter gives the average sunspot cycle as 11 years. Verify this using Figure 15.26 from this chapter which is reproduced here.
27: The escape velocity from any astronomical object can be calculated as v escape = square root (2GM/R) or v escape = (2GM/R) 1/2 Using the data in Appendix E, calculate the escape velocity from the photosphere of the Sun. Since coronal mass ejections escape from the corona, would the escape velocity from there be more or less than from the photosphere?
28: Suppose you observe a major solar flare while astronauts are orbiting Earth. Use the data in the text to calculate how long it will before the charged particles ejected from the Sun during the flare reach them.
29: Suppose an eruptive prominence rises at a speed of 150 km/s. If it does not change speed, how far from the photosphere will it extend after 3 hours? How does this distance compare with the diameter of Earth?
30: From the information in Figure 15.21, estimate the speed with which the particles in the CME in parts (c) and (d) are moving away from the Sun.

