Chapter 20 Electric Current, Resistance, and Ohm’s Law
20.3 Resistance and Resistivity
Summary
- Explain the concept of resistivity.
- Use resistivity to calculate the resistance of specified configurations of material.
- Use the thermal coefficient of resistivity to calculate the change of resistance with temperature.
Material and Shape Dependence of Resistance
The resistance of an object depends on its shape and the material of which it is composed. The cylindrical resistor in Figure 1 is easy to analyze, and, by so doing, we can gain insight into the resistance of more complicated shapes. As you might expect, the cylinder’s electric resistance [latex]{R}[/latex] is directly proportional to its length [latex]{L}[/latex], similar to the resistance of a pipe to fluid flow. The longer the cylinder, the more collisions charges will make with its atoms. The greater the diameter of the cylinder, the more current it can carry (again similar to the flow of fluid through a pipe). In fact, [latex]{R}[/latex] is inversely proportional to the cylinder’s cross-sectional area [latex]{A}[/latex].
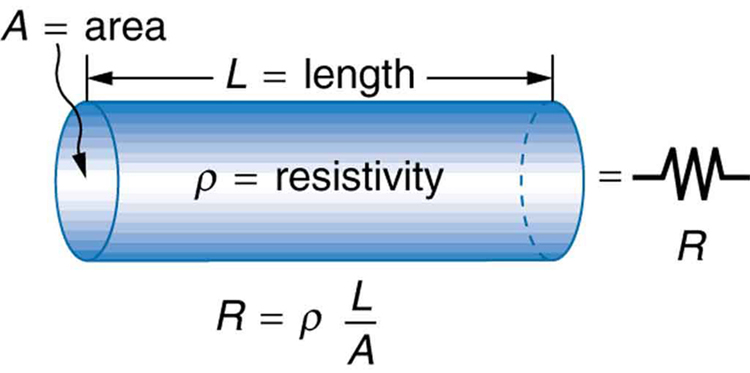
For a given shape, the resistance depends on the material of which the object is composed. Different materials offer different resistance to the flow of charge. We define the resistivity [latex]{\rho}[/latex] of a substance so that the resistance [latex]{R}[/latex] of an object is directly proportional to [latex]{\rho}[/latex]. Resistivity [latex]{\rho}[/latex] is an intrinsic property of a material, independent of its shape or size. The resistance [latex]{R}[/latex] of a uniform cylinder of length [latex]{L}[/latex], of cross-sectional area [latex]{A}[/latex], and made of a material with resistivity [latex]{\rho}[/latex], is
Table 1 gives representative values of [latex]{\rho}[/latex]. The materials listed in the table are separated into categories of conductors, semiconductors, and insulators, based on broad groupings of resistivities. Conductors have the smallest resistivities, and insulators have the largest; semiconductors have intermediate resistivities. Conductors have varying but large free charge densities, whereas most charges in insulators are bound to atoms and are not free to move. Semiconductors are intermediate, having far fewer free charges than conductors, but having properties that make the number of free charges depend strongly on the type and amount of impurities in the semiconductor. These unique properties of semiconductors are put to use in modern electronics, as will be explored in later chapters.
| Material | Resistivity [latex]{\rho (\Omega \cdot \;\text{m})}[/latex] |
|---|---|
| Conductors | |
| Silver | [latex]{1.59 \times 10^{-8}}[/latex] |
| Copper | [latex]{1.72 \times 10^{-8}}[/latex] |
| Gold | [latex]{2.44 \times 10^{-8}}[/latex] |
| Aluminum | [latex]{2.65 \times 10^{-8}}[/latex] |
| Tungsten | [latex]{5.6 \times 10^{-8}}[/latex] |
| Iron | [latex]{9.71 \times 10^{-8}}[/latex] |
| Platinum | [latex]{10.6 \times 10^{-8}}[/latex] |
| Steel | [latex]{20 \times 10^{-8}}[/latex] |
| Lead | [latex]{22 \times 10^{-8}}[/latex] |
| Manganin (Cu, Mn, Ni alloy) | [latex]{44 \times 10^{-8}}[/latex] |
| Constantan (Cu, Ni alloy) | [latex]{49 \times 10^{-8}}[/latex] |
| Mercury | [latex]{96 \times 10^{-8}}[/latex] |
| Nichrome (Ni, Fe, Cr alloy) | [latex]{100 \times 10^{-8}}[/latex] |
| Semiconductors1 | |
| Carbon (pure) | [latex]{3.5 \times 10^5}[/latex] |
| Carbon | [latex]{(3.5 - 60) \times 10^5}[/latex] |
| Germanium (pure) | [latex]{600 \times 10^{-3}}[/latex] |
| Germanium | [latex]{(1-600) \times 10^{-3}}[/latex] |
| Silicon (pure) | [latex]{2300}[/latex] |
| Silicon | [latex]{0.1-2300}[/latex] |
| Insulators | |
| Amber | [latex]{5 \times 10^{14}}[/latex] |
| Glass | [latex]{10^9 - 10^{14}}[/latex] |
| Lucite | [latex]{>10^{13}}[/latex] |
| Mica | [latex]{10^{11} - 10^{15}}[/latex] |
| Quartz (fused) | [latex]{75 \times 10^{16}}[/latex] |
| Rubber (hard) | [latex]{10^{13} - 10^{16}}[/latex] |
| Sulfur | [latex]{10^{15}}[/latex] |
| Teflon | [latex]{>10^{13}}[/latex] |
| Wood | [latex]{10^8 - 10^{11}}[/latex] |
| Table 1. Resistivities [latex]{\rho}[/latex] of Various materials at 20ºC | |
Example 1: Calculating Resistor Diameter: A Headlight Filament
A car headlight filament is made of tungsten and has a cold resistance of [latex]{0.350 \;\Omega}[/latex]. If the filament is a cylinder 4.00 cm long (it may be coiled to save space), what is its diameter?
Strategy
We can rearrange the equation [latex]{R = \frac{\rho L}{A}}[/latex] to find the cross-sectional area [latex]{A}[/latex] of the filament from the given information. Then its diameter can be found by assuming it has a circular cross-section.
Solution
The cross-sectional area, found by rearranging the expression for the resistance of a cylinder given in [latex]{R = \frac{\rho L}{A}}[/latex], is
Substituting the given values, and taking [latex]{\rho}[/latex] from Table 1, yields
The area of a circle is related to its diameter [latex]{D}[/latex] by
Solving for the diameter [latex]{D}[/latex], and substituting the value found for [latex]{A}[/latex], gives
Discussion
The diameter is just under a tenth of a millimeter. It is quoted to only two digits, because [latex]{\rho}[/latex] is known to only two digits.
Temperature Variation of Resistance
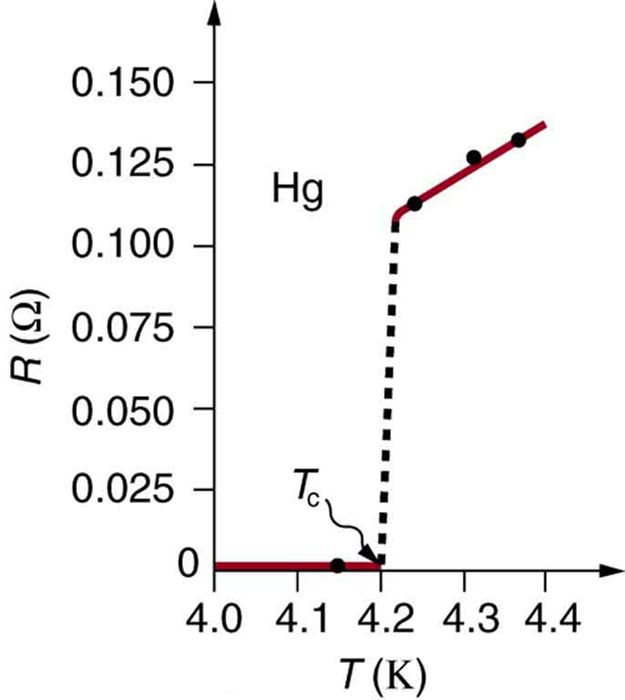
The resistivity of all materials depends on temperature. Some even become superconductors (zero resistivity) at very low temperatures. (See Figure 2.) Conversely, the resistivity of conductors increases with increasing temperature. Since the atoms vibrate more rapidly and over larger distances at higher temperatures, the electrons moving through a metal make more collisions, effectively making the resistivity higher. Over relatively small temperature changes (about 100ºC or less), resistivity [latex]{\rho}[/latex] varies with temperature change [latex]{\Delta T}[/latex] as expressed in the following equation
where [latex]{\rho_0}[/latex] is the original resistivity and [latex]{\alpha}[/latex] is the temperature coefficient of resistivity. (See the values of [latex]{\alpha}[/latex] in Table 2 below.) For larger temperature changes, [latex]{\alpha}[/latex] may vary or a nonlinear equation may be needed to find [latex]{\rho}[/latex]. Note that [latex]{\alpha}[/latex] is positive for metals, meaning their resistivity increases with temperature. Some alloys have been developed specifically to have a small temperature dependence. Manganin (which is made of copper, manganese and nickel), for example, has [latex]{\alpha}[/latex] close to zero (to three digits on the scale in Table 2), and so its resistivity varies only slightly with temperature. This is useful for making a temperature-independent resistance standard, for example.
| Material | Coefficient [latex]{\alpha}[/latex](1/°C)2 |
|---|---|
| Conductors | |
| Silver | [latex]{3.8 \times 10^{-3}}[/latex] |
| Copper | [latex]{3.9 \times 10^{-3}}[/latex] |
| Gold | [latex]{3.4 \times 10^{-3}}[/latex] |
| Aluminum | [latex]{3.9 \times 10^{-3}}[/latex] |
| Tungsten | [latex]{4.5 \times 10^{-3}}[/latex] |
| Iron | [latex]{5.0 \times 10^{-3}}[/latex] |
| Platinum | [latex]{3.93 \times 10^{-3}}[/latex] |
| Lead | [latex]{3.9 \times 10^{-3}}[/latex] |
| Manganin (Cu, Mn, Ni alloy) | [latex]{0.000 \times 10^{-3}}[/latex] |
| Constantan (Cu, Ni alloy) | [latex]{0.002 \times 10^{-3}}[/latex] |
| Mercury | [latex]{0.89 \times 10^{-3}}[/latex] |
| Nichrome (Ni, Fe, Cr alloy) | [latex]{0.4 \times 10^{-3}}[/latex] |
| Semiconductors | |
| Carbon (pure) | [latex]{-0.5 \times 10^{-3}}[/latex] |
| Germanium (pure) | [latex]{-50 \times 10^{-3}}[/latex] |
| Silicon (pure) | [latex]{-70 \times 10^{-3}}[/latex] |
| Table 2: Tempature Coefficients of Resistivity [latex]{\alpha}[/latex] | |
Note also that [latex]{\alpha}[/latex] is negative for the semiconductors listed in Table 2, meaning that their resistivity decreases with increasing temperature. They become better conductors at higher temperature, because increased thermal agitation increases the number of free charges available to carry current. This property of decreasing [latex]{\rho}[/latex] with temperature is also related to the type and amount of impurities present in the semiconductors.
The resistance of an object also depends on temperature, since [latex]{R_0}[/latex] is directly proportional to [latex]{\rho}[/latex]. For a cylinder we know [latex]{R = \rho L/A}[/latex], and so, if [latex]{L}[/latex] and [latex]{A}[/latex] do not change greatly with temperature, [latex]{R}[/latex] will have the same temperature dependence as [latex]{\rho}[/latex]. (Examination of the coefficients of linear expansion shows them to be about two orders of magnitude less than typical temperature coefficients of resistivity, and so the effect of temperature on [latex]{L}[/latex] and [latex]{A}[/latex] is about two orders of magnitude less than on [latex]{\rho}[/latex].) Thus,
is the temperature dependence of the resistance of an object, where [latex]{R_0}[/latex] is the original resistance and [latex]{R}[/latex] is the resistance after a temperature change [latex]{\Delta T}[/latex]. Numerous thermometers are based on the effect of temperature on resistance. (See Figure 3.) One of the most common is the thermistor, a semiconductor crystal with a strong temperature dependence, the resistance of which is measured to obtain its temperature. The device is small, so that it quickly comes into thermal equilibrium with the part of a person it touches.
Example 2: Calculating Resistance: Hot-Filament Resistance
Although caution must be used in applying [latex]{ \rho = \rho_0(1 + \alpha \Delta T)}[/latex] and [latex]{R = R_0(1 + \alpha \Delta T)}[/latex] for temperature changes greater than 100ºC, for tungsten the equations work reasonably well for very large temperature changes. What, then, is the resistance of the tungsten filament in the previous example if its temperature is increased from room temperature (20ºC) to a typical operating temperature of 2850ºC?
Strategy
This is a straightforward application of [latex]{R = R_0(1 + \alpha \Delta T)}[/latex], since the original resistance of the filament was given to be [latex]{R_0 = 0.350 \;\Omega}[/latex], and the temperature change is [latex]{\Delta T = 2830 ^{\circ} \text{C}}[/latex].
Solution
The hot resistance [latex]{R}[/latex] is obtained by entering known values into the above equation:
Discussion
This value is consistent with the headlight resistance example in Example 1 Chapter 20.2 Ohm’s Law: Resistance and Simple Circuits.
PhET Explorations: Resistance in a Wire
Learn about the physics of resistance in a wire. Change its resistivity, length, and area to see how they affect the wire's resistance. The sizes of the symbols in the equation change along with the diagram of a wire.

Section Summary
- The resistance [latex]{R}[/latex] of a cylinder of length [latex]{L}[/latex] and cross-sectional area [latex]{A}[/latex] is [latex]{R = \frac{\rho L}{A}}[/latex], where [latex]{\rho}[/latex] is the resistivity of the material.
- Values of [latex]{\rho}[/latex] in Table 1 show that materials fall into three groups—conductors, semiconductors, and insulators.
- Temperature affects resistivity; for relatively small temperature changes [latex]{\Delta T}[/latex], resistivity is [latex]{\rho = \rho_0(1 + \alpha \Delta T)}[/latex], where [latex]{\rho_0}[/latex] is the original resistivity and αα is the temperature coefficient of resistivity.
- Table 2 gives values for [latex]{\alpha}[/latex], the temperature coefficient of resistivity.
- The resistance [latex]{R}[/latex] of an object also varies with temperature: [latex]{R = R_0(1 + \alpha \Delta T)}[/latex], where [latex]{R_0}[/latex] is the original resistance, and [latex]{R}[/latex] is the resistance after the temperature change.
Conceptual Questions
1: In which of the three semiconducting materials listed in Table 1 do impurities supply free charges? (Hint: Examine the range of resistivity for each and determine whether the pure semiconductor has the higher or lower conductivity.)
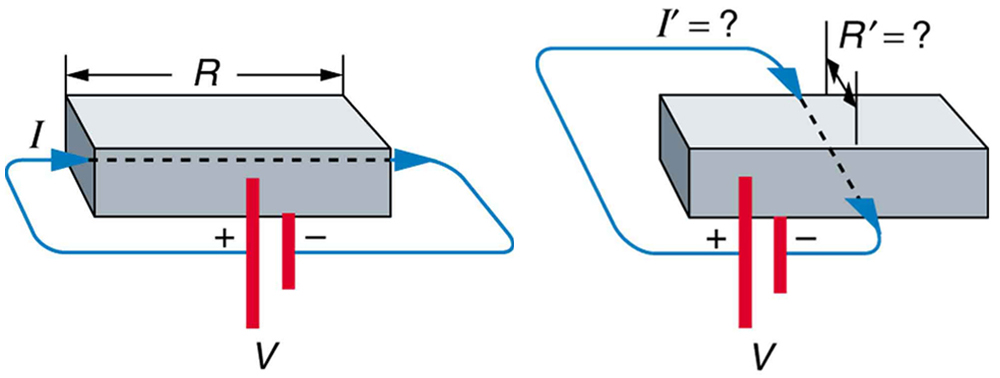
2: Does the resistance of an object depend on the path current takes through it? Consider, for example, a rectangular bar—is its resistance the same along its length as across its width? (See Figure 5.)
3: If aluminum and copper wires of the same length have the same resistance, which has the larger diameter? Why?
4: Explain why [latex]{R = R_0 (1 + \alpha \Delta T)}[/latex] for the temperature variation of the resistance [latex]{R}[/latex] of an object is not as accurate as [latex]{\rho = \rho_0(1 + \alpha \Delta T)}[/latex], which gives the temperature variation of resistivity [latex]{\rho}[/latex].
Problems & Exercises
1: What is the resistance of a 20.0-m-long piece of 12-gauge copper wire having a 2.053-mm diameter?
2: The diameter of 0-gauge copper wire is 8.252 mm. Find the resistance of a 1.00-km length of such wire used for power transmission.
3: If the 0.100-mm diameter tungsten filament in a light bulb is to have a resistance of [latex]{0.200 \;\Omega}[/latex] at 20.0ºC, how long should it be?
4: Find the ratio of the diameter of aluminum to copper wire, if they have the same resistance per unit length (as they might in household wiring).
5: What current flows through a 2.54-cm-diameter rod of pure silicon that is 20.0 cm long, when [latex]{1.00 \times 10^3 \;\text{V}}[/latex] is applied to it? (Such a rod may be used to make nuclear-particle detectors, for example.)
6: (a) To what temperature must you raise a copper wire, originally at 20.0ºC, to double its resistance, neglecting any changes in dimensions? (b) Does this happen in household wiring under ordinary circumstances?
7: A resistor made of Nichrome wire is used in an application where its resistance cannot change more than 1.00% from its value at 20.0ºC. Over what temperature range can it be used?
8: Of what material is a resistor made if its resistance is 40.0% greater at 100ºC than at 20.0ºC?
9: An electronic device designed to operate at any temperature in the range from –10.0ºC to 55.0ºC contains pure carbon resistors. By what factor does their resistance increase over this range?
10: (a) Of what material is a wire made, if it is 25.0 m long with a 0.100 mm diameter and has a resistance of [latex]{77.7 \;\Omega}[/latex] at 20.0ºC? (b) What is its resistance at 150ºC?
11: Assuming a constant temperature coefficient of resistivity, what is the maximum percent decrease in the resistance of a constantan wire starting at 20.0ºC?
12: A wire is drawn through a die, stretching it to four times its original length. By what factor does its resistance increase?
13: A copper wire has a resistance of [latex]{0.500 \;\Omega}[/latex] at 20.0ºC, and an iron wire has a resistance of [latex]{0.525 \;\Omega}[/latex] at the same temperature. At what temperature are their resistances equal?
14: (a) Digital medical thermometers determine temperature by measuring the resistance of a semiconductor device called a thermistor (which has [latex]{\alpha = -0.0600/^{\circ} \text{C}}[/latex]) when it is at the same temperature as the patient. What is a patient’s temperature if the thermistor’s resistance at that temperature is 82.0% of its value at 37.0ºC (normal body temperature)? (b) The negative value for [latex]{\alpha}[/latex] may not be maintained for very low temperatures. Discuss why and whether this is the case here. (Hint: Resistance can’t become negative.)
15: Integrated Concepts
(a) Redo Exercise 2 taking into account the thermal expansion of the tungsten filament. You may assume a thermal expansion coefficient of [latex]{12 \times 10^{-6}/^{\circ} \text{C}}[/latex]. (b) By what percentage does your answer differ from that in the example?
16: Unreasonable Results
(a) To what temperature must you raise a resistor made of constantan to double its resistance, assuming a constant temperature coefficient of resistivity? (b) To cut it in half? (c) What is unreasonable about these results? (d) Which assumptions are unreasonable, or which premises are inconsistent?
Glossary
- resistivity
- an intrinsic property of a material, independent of its shape or size, directly proportional to the resistance, denoted by ρ
- temperature coefficient of resistivity
- an empirical quantity, denoted by α, which describes the change in resistance or resistivity of a material with temperature
Solutions
Problems & Exercises
1: [latex]{0.104 \;\Omega}[/latex]
3: [latex]{2.8 \times 10^{-2} \;\text{m}}[/latex]
5: [latex]{1.10 \times 10^{-3} \;\textbf{A}}[/latex]
7: −5ºC to 45ºC
9: 1.03
11: 0.06%
13: −17ºC
15: (a) [latex]{4.7 \;\Omega}[/latex] (total)
(b) 3.0% decrease

