6 Chapter 6: Summary of Applications of Airfoil Aerodynamics
Additionally, it is important to recall that ![]() also drives the lift-curve-slope. This is driven by the Gluert compressibility factor (
also drives the lift-curve-slope. This is driven by the Gluert compressibility factor (![]() ). Using this character, we can approximate an airfoil lift using the Gluart correction as follows:
). Using this character, we can approximate an airfoil lift using the Gluart correction as follows:
(1) ![]()
A typically change in lift character is provided in the Fig. below.

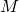 on
on 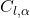 and
and 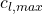 .
.Lastly, non-linear aerodynamics also demands some attention. This is typically driven by flow separation on the airfoil itself. In general, stall occurs when flow separation occurs over the entire airfoil upper surface.
Using this character, we can approximate an airfoil lift using Kirchoff model as follows:
(2) ![]()
In general, the lift character becomes modified as follows:
Zero lift angle of attack (![]() ) or
) or ![]() at
at ![]() (
(![]() ).
).
The zero-lift angle of attack or lift at ![]() correlates to the camber. This is a factor that tends to relate to drag reduction or finding airfoils that function better for the flight envelope of the aircraft. In general, this factor drives a different lift coefficient function through the following relationship:
correlates to the camber. This is a factor that tends to relate to drag reduction or finding airfoils that function better for the flight envelope of the aircraft. In general, this factor drives a different lift coefficient function through the following relationship:
(3) ![]()
Visually, this is presented in the Fig. below. Note that the calculation of this can come thin airfoil theory.
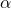 and
and 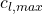 with camber.
with camber.If we pull in the other aspects we have effects of flow separation (Kirchhoff, Eq. 2):
(4) ![]()
as well as compressible flow (Glauret, Eq 1):
(5) ![]()
Equation 5 essentially pull all the methods together.
Max Lift Coefficient (![]() )
)
This is the maximum lift coefficient that an airfoil obtains without flaps or other lift enhancement devices. This quantity relates to the stall speed, wing area, and other factors that ensure aircraft flight. ![]() is highly dependent on flow separation which is affected by viscous effects, laminar versus turbulence boundary layers, and shock-induced stall. Hence, this feature inversely correlates to both
is highly dependent on flow separation which is affected by viscous effects, laminar versus turbulence boundary layers, and shock-induced stall. Hence, this feature inversely correlates to both ![]() and
and ![]() .
. ![]() also inversely correlates to surface roughness (insects, manufacturing imperfections, erosion) that tend to reduce laminar flow to prevent flow separation (which is what vortex generators tend to do).
also inversely correlates to surface roughness (insects, manufacturing imperfections, erosion) that tend to reduce laminar flow to prevent flow separation (which is what vortex generators tend to do).
This figure indicates the changes in ![]() with various
with various ![]() values.
values.

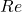 on
on 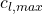 .
.Min Drag Coefficient (![]() )
)
This is the minimum drag coefficient experienced by an airfoil. This tends to occur near the zero-lift angle of attack. The value is highly sensitive to the boundary layer character (laminar versus turbulent) and the length laminar flow is obtained. Because of this, the value is correlated to the length of laminar flow and is inversely correlated to ![]() , roughness, and
, roughness, and ![]() .
.
Drag Bucket
This is the minimum drag coefficient experienced by an airfoil. This tends to occur near the zero-lift angle of attack. The value is highly sensitive to the boundary layer character (laminar versus turbulent) and the length laminar flow is obtained. Because of this, the value is correlated to the length of laminar flow and is inversely correlated to ![]() , roughness, and
, roughness, and ![]() .
.
