Chapter 4 The Second Law of Thermodynamics
Chapter Review
OpenStax and Paula Herrera-Siklody
Key Terms | Key Equations | Summary | Conceptual Questions | Problems | Additional Problems | Challenge Problems
Key Terms
Carnot cycle: cycle that consists of two isotherms at the temperatures of two reservoirs and two adiabatic processes connecting the isotherms
Carnot engine: Carnot heat engine, refrigerator, or heat pump that operates on a Carnot cycle
Carnot principle: principle governing the efficiency or performance of a heat device operating on a
Carnot cycle: any reversible heat device working between two reservoirs must have the same efficiency or performance coefficient, greater than that of an irreversible heat device operating between the same two reservoirs
Clausius statement of the second law of thermodynamics: heat never flows spontaneously from a colder object to a hotter object
coefficient of performance: measure of effectiveness of a refrigerator or heat pump
cold reservoir: sink of heat used by a heat engine
disorder: measure of order in a system; the greater the disorder is, the higher the entropy
efficiency (e): output work from the engine over the input heat to the engine from the hot reservoir
entropy: state function of the system that changes when heat is transferred between the system and the environment
entropy statement of the second law of thermodynamics: entropy of a closed system or the entire universe never decreases
heat engine: device that converts heat into work
heat pump: device that delivers heat to a hot reservoir
hot reservoir: source of heat used by a heat engine
irreversibility: phenomenon associated with a natural process
irreversible process: process in which neither the system nor its environment can be restored to their original states at the same time
isentropic: reversible adiabatic process where the process is frictionless and no heat is transferred
Kelvin statement of the second law of thermodynamics: it is impossible to convert the heat from a single source into work without any other effect
perfect engine: engine that can convert heat into work with 100% efficiency
perfect refrigerator (heat pump): refrigerator (heat pump) that can remove (dump) heat without any input of work
refrigerator: device that removes heat from a cold reservoir
reversible process: process in which both the system and the external environment theoretically can be returned to their original states
third law of thermodynamics: absolute zero temperature cannot be reached through any finite number of cooling steps
Key Equations
| Result of energy conservation | |
| Efficiency of a heat engine | |
| Coefficient of performance of a refrigerator | |
| Coefficient of performance of a heat pump | |
| Resulting efficiency of a Carnot cycle | |
| Performance coefficient of a reversible refrigerator | |
| Performance coefficient of a reversible heat pump | |
| Entropy of a system undergoing a reversible process at a constant temperature | |
| Change of entropy of a system under a reversible process | |
| Entropy of a system undergoing any complete reversible cyclic process | |
| Change of entropy of a closed system under an irreversible process | |
| Change in entropy of the system along an isotherm |
Summary
4.1 Reversible and Irreversible Processes
- A reversible process is one in which both the system and its environment can return to exactly the states they were in by following the reverse path.
- An irreversible process is one in which the system and its environment cannot return together to exactly the states that they were in.
- The irreversibility of any natural process results from the second law of thermodynamics.
4.2 Heat Engines
- The work done by a heat engine is the difference between the heat absorbed from the hot reservoir and the heat discharged to the cold reservoir, that is, [latex]W=Q_h - Q_c[/latex].
- The ratio of the work done by the engine and the heat absorbed from the hot reservoir provides the efficiency of the engine, that is, [latex]e=W/Q_{h}=1 - Q_{c}/Q_{h}[/latex].
4.3 Refrigerators and Heat Pumps
- A refrigerator or a heat pump is a heat engine run in reverse.
- The focus of a refrigerator is on removing heat from the cold reservoir with a coefficient of performance [latex]K_R[/latex].
- The focus of a heat pump is on dumping heat to the hot reservoir with a coefficient of performance [latex]K_P[/latex].
4.4 Statements of the Second Law of Thermodynamics
- The Kelvin statement of the second law of thermodynamics: It is impossible to convert the heat from a single source into work without any other effect.
- The Kelvin statement and Clausius statement of the second law of thermodynamics are equivalent.
4.5 The Carnot Cycle
- The Carnot cycle is the most efficient engine for a reversible cycle designed between two reservoirs.
- The Carnot principle is another way of stating the second law of thermodynamics.
4.6 Entropy
- The change in entropy for a reversible process at constant temperature is equal to the heat divided by the temperature. The entropy change of a system under a reversible process is given by
- A system’s change in entropy between two states is independent of the reversible thermodynamic path taken by the system when it makes a transition between the states.
4.7 Entropy on a Microscopic Scale
- Entropy can be related to how disordered a system is—the more it is disordered, the higher is its entropy. In any irreversible process, the universe becomes more disordered.
- According to the third law of thermodynamics, absolute zero temperature is unreachable.
Conceptual Questions
4.1 Reversible and Irreversible Processes
1. State an example of a process that occurs in nature that is as close to reversible as it can be.
4.2 Heat Engines
2. Explain in practical terms why efficiency is defined as [latex]W/Q_h[/latex].
4.3 Refrigerators and Heat Pumps
3. If the refrigerator door is left open, what happens to the temperature of the kitchen?
4. Is it possible for the efficiency of a reversible engine to be greater than 1.0? Is it possible for the coefficient of performance of a reversible refrigerator to be less than 1.0?
4.4 Statements of the Second Law of Thermodynamics
5. In the text, we showed that if the Clausius statement is false, the Kelvin statement must also be false. Now show the reverse, such that if the Kelvin statement is false, it follows that the Clausius statement is false.
6. Why don’t we operate ocean liners by extracting heat from the ocean or operate airplanes by extracting heat from the atmosphere?
7. Discuss the practical advantages and disadvantages of heat pumps and electric heating.
8. The energy output of a heat pump is greater than the energy used to operate the pump. Why doesn’t this statement violate the first law of thermodynamics?
9. Speculate as to why nuclear power plants are less efficient than fossil-fuel plants based on temperature arguments.
10. An ideal gas goes from state ([latex]p_i[/latex], [latex]V_i[/latex]) to state ([latex]p_f[/latex], [latex]V_f[/latex]) when it is allowed to expand freely. Is it possible to represent the actual process on a pV diagram? Explain.
4.5 The Carnot Cycle
11. To increase the efficiency of a Carnot engine, should the temperature of the hot reservoir be raised or lowered? What about the cold reservoir?
12. How could you design a Carnot engine with 100% efficiency?
13. What type of processes occur in a Carnot cycle?
4.6 Entropy
14. Does the entropy increase for a Carnot engine for each cycle?
15. Is it possible for a system to have an entropy change if it neither absorbs nor emits heat during a reversible transition? What happens if the process is irreversible?
4.7 Entropy on a Microscopic Scale
16. Are the entropy changes of the systems in the following processes positive or negative?
(a) water vapor that condenses on a cold surface;
(b) gas in a container that leaks into the surrounding atmosphere;
(c) an ice cube that melts in a glass of lukewarm water;
(d) the lukewarm water of part (c);
(e) a real heat engine performing a cycle;
(f) food cooled in a refrigerator.
17. Discuss the entropy changes in the systems of Question 21.10 in terms of disorder.
Problems
4.1 Reversible and Irreversible Processes
18. A tank contains 111.0 g chlorine gas ([latex]\text{Cl}_2[/latex]), which is at temperature 82.0°C and absolute pressure [latex]5.70 \times 10^{5}\text{Pa}[/latex]. The temperature of the air outside the tank is 20.0°C. The molar mass of [latex]\text{Cl}_2[/latex] is 70.9 g/mol.
(a) What is the volume of the tank?
(b) What is the internal energy of the gas?
(c) What is the work done by the gas if the temperature and pressure inside the tank drop to 31.0°C and [latex]3.80 \times 10^{5}\text{Pa}[/latex], respectively, due to a leak?
19. A mole of ideal monatomic gas at 0°C and 1.00 atm is warmed up to expand isobarically to triple its volume. How much heat is transferred during the process?
20. A mole of an ideal gas at pressure 4.00 atm and temperature 298 K expands isothermally to double its volume. What is the work done by the gas?
21. After a free expansion to quadruple its volume, a mole of ideal diatomic gas is compressed back to its original volume isobarically and then cooled down to its original temperature. What is the minimum heat removed from the gas in the final step to restoring its state?
4.2 Heat Engines
22. An engine is found to have an efficiency of 0.40. If it does 200 J of work per cycle, what are the corresponding quantities of heat absorbed and discharged?
23. In performing 100.0 J of work, an engine discharges 50.0 J of heat. What is the efficiency of the engine?
24. An engine with an efficiency of 0.30 absorbs 500 J of heat per cycle.
(a) How much work does it perform per cycle?
(b) How much heat does it discharge per cycle?
25. It is found that an engine discharges 100.0 J while absorbing 125.0 J each cycle of operation.
(a) What is the efficiency of the engine?
(b) How much work does it perform per cycle?
26. The temperature of the cold reservoir of the engine is 300 K. It has an efficiency of 0.30 and absorbs 500 J of heat per cycle.
(a) How much work does it perform per cycle?
(b) How much heat does it discharge per cycle?
27. An engine absorbs three times as much heat as it discharges. The work done by the engine per cycle is 50 J. Calculate (a) the efficiency of the engine, (b) the heat absorbed per cycle, and (c) the heat discharged per cycle.
28. A coal power plant consumes 100,000 kg of coal per hour and produces 500 MW of power. If the heat of combustion of coal is 30 MJ/kg, what is the efficiency of the power plant?
4.3 Refrigerators and Heat Pumps
29. A refrigerator has a coefficient of performance of 3.0. (a) If it requires 200 J of work per cycle, how much heat per cycle does it remove the cold reservoir? (b) How much heat per cycle is discarded to the hot reservoir?
30. During one cycle, a refrigerator removes 500 J from a cold reservoir and discharges 800 J to its hot reservoir.
(a) What is its coefficient of performance?
(b) How much work per cycle does it require to operate?
31. If a refrigerator discards 80 J of heat per cycle and its coefficient of performance is 6.0, what are
(a) the quantity off heat it removes per cycle from a cold reservoir and
(b) the amount of work per cycle required for its operation?
32. A refrigerator has a coefficient of performance of 3.0.
(a) If it requires 200 J of work per cycle, how much heat per cycle does it remove the cold reservoir?
(b) How much heat per cycle is discarded to the hot reservoir?
4.5 The Carnot Cycle
33. The temperature of the cold and hot reservoirs between which a Carnot refrigerator operates are −73°C and 270°C, respectively. Which is its coefficient of performance?
34. Suppose a Carnot refrigerator operates between [latex]T_c[/latex] and [latex]T_h[/latex]. Calculate the amount of work required to extract 1.0 J of heat from the cold reservoir if
(a) [latex]T_c = 7 \text{°C}[/latex], [latex]T_h = 27 \text{°C}[/latex]
(b) [latex]T_c = -73 \text{°C}[/latex], [latex]T_h = 27 \text{°C}[/latex];
(c) [latex]T_c = − 173 {°C}[/latex], [latex]T_h = 27 {°C}[/latex]; and
(d) [latex]T_c = −273 \text{°C}[/latex], [latex]T_h = 27 \text {°C}[/latex].
35. A Carnot engine operates between reservoirs at 600 and 300 K. If the engine absorbs 100 J per cycle at the hot reservoir, what is its work output per cycle?
36. A 500-W motor operates a Carnot refrigerator between −5°C and 30°C. (a) What is the amount of heat per second extracted from the inside of the refrigerator? (b) How much heat is exhausted to the outside air per second?
37. Sketch a Carnot cycle on a temperature-volume diagram.
38. A Carnot heat pump operates between 0°C and 20°C. How much heat is exhausted into the interior of a house for every 1.0 J of work done by the pump?
39. An engine operating between heat reservoirs at 20°C and 200°C extracts 1000 J per cycle from the hot reservoir.
(a) What is the maximum possible work that engine can do per cycle?
(b) For this maximum work, how much heat is exhausted to the cold reservoir per cycle?
40. Suppose a Carnot engine can be operated between two reservoirs as either a heat engine or a refrigerator. How is the coefficient of performance of the refrigerator related to the efficiency of the heat engine?
41. A Carnot engine is used to measure the temperature of a heat reservoir. The engine operates between the heat reservoir and a reservoir consisting of water at its triple point.
(a) If 400 J per cycle are removed from the heat reservoir while 200 J per cycle are deposited in the triple-point reservoir, what is the temperature of the heat reservoir?
(b) If 400 J per cycle are removed from the triple-point reservoir while 200 J per cycle are deposited in the heat reservoir, what is the temperature of the heat reservoir?
42. What is the minimum work required of a refrigerator if it is to extract 50 J per cycle from the inside of a freezer at −10°C and exhaust heat to the air at 25°C?
4.6 Entropy
43. Two hundred joules of heat are removed from a heat reservoir at a temperature of 200 K. What is the entropy change of the reservoir?
44. In an isothermal reversible expansion at 27°C, an ideal gas does 20 J of work. What is the entropy change of the gas?
45. An ideal gas at 300 K is compressed isothermally to one-fifth its original volume. Determine the entropy change per mole of the gas.
46. What is the entropy change of 10 g of steam at 100°C when it condenses to water at the same temperature?
47. A metal rod is used to conduct heat between two reservoirs at temperatures [latex]T_h[/latex] and [latex]T_c[/latex], respectively. When an amount of heat Q flows through the rod from the hot to the cold reservoir, what is the net entropy change of the rod, the hot reservoir, the cold reservoir, and the universe?
48. For the Carnot cycle of Figure 4.12, what is the entropy change of the hot reservoir, the cold reservoir, and the universe?
49. A 5.0-kg piece of lead at a temperature of 600°C is placed in a lake whose temperature is 15°C. Determine the entropy change of (a) the lead piece, (b) the lake, and (c) the universe.
50. One mole of an ideal gas doubles its volume in a reversible isothermal expansion. (a) What is the change in entropy of the gas? (b) If 1500 J of heat are added in this process, what is the temperature of the gas?
51. One mole of an ideal monatomic gas is confined to a rigid container. When heat is added reversibly to the gas, its temperature changes from [latex]T_1[/latex] to [latex]T_2[/latex]. (a) How much heat is added? (b) What is the change in entropy of the gas?
52. (a) A 5.0-kg rock at a temperature of 20°C is dropped into a shallow lake also at 20°C from a height of [latex]1.0 \times 10^{3}\text{m}[/latex]. What is the resulting change in entropy of the universe? (b) If the temperature of the rock is 100°C when it is dropped, what is the change of entropy of the universe? Assume that air friction is negligible (not a good assumption) and that [latex]c = 860 \text{J/kg} \cdot \text{K}[/latex] is the specific heat of the rock.
4.7 Entropy on a Microscopic Scale
53. A copper rod of cross-sectional area [latex]5.0 \text{cm}^{2}[/latex] and length 5.0 m conducts heat from a heat reservoir at 373 K to one at 273 K. What is the time rate of change of the universe’s entropy for this process?
54. Fifty grams of water at 20°C is heated until it becomes vapor at 100°C. Calculate the change in entropy of the water in this process.
55. Fifty grams of water at 0°C are changed into vapor at 100°C. What is the change in entropy of the water in this process?
56. In an isochoric process, heat is added to 10 mol of monoatomic ideal gas whose temperature increases from 273 to 373 K. What is the entropy change of the gas?
57. Two hundred grams of water at 0°C is brought into contact with a heat reservoir at 80°C. After thermal equilibrium is reached, what is the temperature of the water? Of the reservoir? How much heat has been transferred in the process? What is the entropy change of the water? Of the reservoir? What is the entropy change of the universe?
58. Suppose that the temperature of the water in the previous problem is raised by first bringing it to thermal equilibrium with a reservoir at a temperature of 40°C and then with a reservoir at 80°C. Calculate the entropy changes of (a) each reservoir, (b) of the water, and (c) of the universe.
59. Two hundred grams of water at 0°C is brought into contact into thermal equilibrium successively with reservoirs at 20°C, 40°C, 60°C, and 80°C. (a) What is the entropy change of the water? (b) Of the reservoir? (c) What is the entropy change of the universe?
60. (a) Ten grams of H2O starts as ice at 0°C. The ice absorbs heat from the air (just above 0°C) until all of it melts. Calculate the entropy change of the H2O, of the air, and of the universe. (b) Suppose that the air in part (a) is at 20°C rather than 0°C and that the ice absorbs heat until it becomes water at 20°C. Calculate the entropy change of the H2O, of the air, and of the universe. (c) Is either of these processes reversible?
61. The Carnot cycle is represented by the temperature-entropy diagram shown below.
(a) How much heat is absorbed per cycle at the high-temperature reservoir?
(b) How much heat is exhausted per cycle at the low-temperature reservoir?
(c) How much work is done per cycle by the engine?
(d) What is the efficiency of the engine?
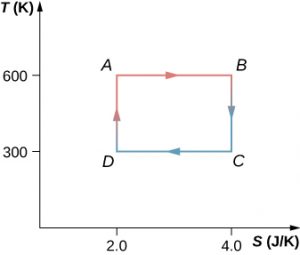
62. A Carnot engine operating between heat reservoirs at 500 and 300 K absorbs 1500 J per cycle at the high-temperature reservoir. (a) Represent the engine’s cycle on a temperature-entropy diagram. (b) How much work per cycle is done by the engine?
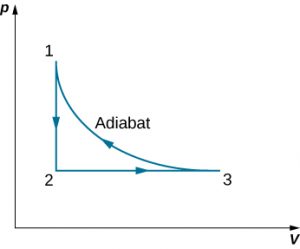
63. A monoatomic ideal gas (n moles) goes through a cyclic process shown below. Find the change in entropy of the gas in each step and the total entropy change over the entire cycle.
64. A Carnot engine has an efficiency of 0.60. When the temperature of its cold reservoir changes, the efficiency drops to 0.55. If initially [latex]T_c = 27\text{°C}[/latex], determine (a) the constant value of [latex]T_h[/latex] and (b) the final value of [latex]T_c[/latex].
65. A Carnot engine performs 100 J of work while discharging 200 J of heat each cycle. After the temperature of the hot reservoir only is adjusted, it is found that the engine now does 130 J of work while discarding the same quantity of heat. (a) What are the initial and final efficiencies of the engine? (b) What is the fractional change in the temperature of the hot reservoir?
66. A Carnot refrigerator exhausts heat to the air, which is at a temperature of 25°C. How much power is used by the refrigerator if it freezes 1.5 g of water per second? Assume the water is at 0°C.
Additional Problems
67. A 300-W heat pump operates between the ground, whose temperature is 0°C, and the interior of a house at 22°C. What is the maximum amount of heat per hour that the heat pump can supply to the house?
68. An engineer must design a refrigerator that does 300 J of work per cycle to extract 2100 J of heat per cycle from a freezer whose temperature is −10°C. What is the maximum air temperature for which this condition can be met? Is this a reasonable condition to impose on the design?
69. A Carnot engine employs 1.5 mol of nitrogen gas as a working substance, which is considered as an ideal diatomic gas with [latex]\gamma = 7.5[/latex] at the working temperatures of the engine. The Carnot cycle goes in the cycle ABCDA with AB being an isothermal expansion. The volume at points A and C of the cycle are [latex]5.0 \times 10^{-3}\text{m}^{3}[/latex] and 0.15 L, respectively. The engine operates between two thermal baths of temperature 500 K and 300 K.
(a) Find the values of volume at B and D.
(b) How much heat is absorbed by the gas in the AB isothermal expansion?
(c) How much work is done by the gas in the AB isothermal expansion?
(d) How much heat is given up by the gas in the CD isothermal expansion?
(e) How much work is done by the gas in the CD isothermal compression?
(f) How much work is done by the gas in the BC adiabatic expansion?
(g) How much work is done by the gas in the DA adiabatic compression?
(h) Find the value of efficiency of the engine based on the net work and heat input. Compare this value to the efficiency of a Carnot engine based on the temperatures of the two baths.
70. A 5.0-kg wood block starts with an initial speed of 8.0 m/s and slides across the floor until friction stops it. Estimate the resulting change in entropy of the universe. Assume that everything stays at a room temperature of 20°C.
71. A system consisting of 20.0 mol of a monoatomic ideal gas is cooled at constant pressure from a volume of 50.0 L to 10.0 L. The initial temperature was 300 K. What is the change in entropy of the gas?
72. A glass beaker of mass 400 g contains 500 g of water at 27°C. The beaker is heated reversibly so that the temperature of the beaker and water rise gradually to 57°C. Find the change in entropy of the beaker and water together.
73. A Carnot engine operates between 550°C and 20°C baths and produces 300 kJ of energy in each cycle. Find the change in entropy of the (a) hot bath and (b) cold bath, in each Carnot cycle?
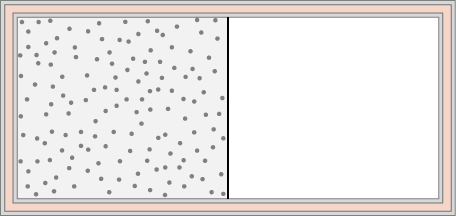
74. An ideal gas at temperature T is stored in the left half of an insulating container of volume V using a partition of negligible volume (see below). What is the entropy change per mole of the gas in each of the following cases?
(a) The partition is suddenly removed and the gas quickly fills the entire container.
(b) A tiny hole is punctured in the partition and after a long period, the gas reaches an equilibrium state such that there is no net flow through the hole.
(c) The partition is moved very slowly and adiabatically all the way to the right wall so that the gas finally fills the entire container.
75. A 0.50-kg piece of aluminum at 250°C is dropped into 1.0 kg of water at 20°C. After equilibrium is reached, what is the net entropy change of the system?
76. Suppose 20 g of ice at 0°C is added to 300 g of water at 60°C. What is the total change in entropy of the mixture after it reaches thermal equilibrium?
77. A heat engine operates between two temperatures such that the working substance of the engine absorbs 5000 J of heat from the high-temperature bath and discharges 3000 J to the low-temperature bath. The rest of the energy is converted into mechanical energy of the turbine. Find (a) the amount of work produced by the engine and (b) the efficiency of the engine.
78. A thermal engine produces 4 MJ of electrical energy while operating between two thermal baths of different temperatures. The working substance of the engine discharges 5 MJ of heat to the cold temperature bath. What is the efficiency of the engine?
79. A coal power plant consumes 100,000 kg of coal per hour and produces 500 MW of power. If the heat of combustion of coal is 30 MJ/kg, what is the efficiency of the power plant?
80. A Carnot engine operates in a Carnot cycle between a heat source at 550°C and a heat sink at 20°C. Find the efficiency of the Carnot engine.
81. A Carnot engine working between two heat baths of temperatures 600 K and 273 K completes each cycle in 5 sec. In each cycle, the engine absorbs 10 kJ of heat. Find the power of the engine.
82. A Carnot cycle working between 100°C and 30°C is used to drive a refrigerator between −10°C and 30°C. How much energy must the Carnot engine produce per second so that the refrigerator is able to discard 10 J of energy per second?
Challenge Problems
83. (a) An infinitesimal amount of heat is added reversibly to a system. By combining the first and second laws, show that [latex]dU = TdS - dW[/latex].
(b) When heat is added to an ideal gas, its temperature and volume change from [latex]T_1[/latex] and [latex]V_1[/latex] to [latex]T_2[/latex] and [latex]V_2[/latex]. Show that the entropy change of n moles of the gas is given by
84. Using the result of the preceding problem, show that for an ideal gas undergoing an adiabatic process, [latex]TV^{\gamma-1}[/latex] is constant.
85. With the help of the two preceding problems, show that [latex]\Delta S[/latex] between states 1 and 2 of n moles an ideal gas is given by
86. A cylinder contains 500 g of helium at 120 atm and 20°C. The valve is leaky, and all the gas slowly escapes isothermally into the atmosphere. Use the results of the preceding problem to determine the resulting change in entropy of the universe.
87. A diatomic ideal gas is brought from an initial equilibrium state at [latex]p_1 = 0.50 \text{atm}[/latex] and [latex]T_1 = 300 \text{K}[/latex] to a final stage with [latex]p_2 = 0.20 \text{atm}[/latex] and [latex]T_1 = 500\text{K}[/latex]. Use the results of the previous problem to determine the entropy change per mole of the gas.
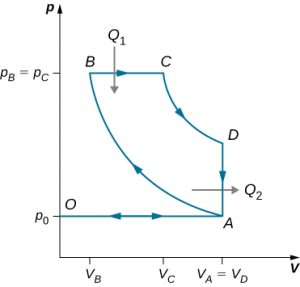
88. The gasoline internal combustion engine operates in a cycle consisting of six parts. Four of these parts involve, among other things, friction, heat exchange through finite temperature differences, and accelerations of the piston; it is irreversible. Nevertheless, it is represented by the ideal reversible Otto cycle, which is illustrated below. The working substance of the cycle is assumed to be air. The six steps of the Otto cycle are as follows:
i. Isobaric intake stroke (OA). A mixture of gasoline and air is drawn into the combustion chamber at atmospheric pressure [latex]p_0[/latex] as the piston expands, increasing the volume of the cylinder from zero to [latex]V_A[/latex].
ii. Adiabatic compression stroke (AB). The temperature of the mixture rises as the piston compresses it adiabatically from a volume [latex]V_A[/latex] to [latex]V_B[/latex].
iii. Ignition at constant volume (BC). The mixture is ignited by a spark. The combustion happens so fast that there is essentially no motion of the piston. During this process, the added heat [latex]Q_1[/latex] causes the pressure to increase from [latex]p_B[/latex] to [latex]p_C[/latex] at the constant volume [latex]V_B (=V_C)[/latex].
iv. Adiabatic expansion (CD). The heated mixture of gasoline and air expands against the piston, increasing the volume from [latex]V_C[/latex] to [latex]V_D[/latex]. This is called the power stroke, as it is the part of the cycle that delivers most of the power to the crankshaft.
v. Constant-volume exhaust (DA). When the exhaust valve opens, some of the combustion products escape. There is almost no movement of the piston during this part of the cycle, so the volume remains constant at [latex]V_A(=V_D)[/latex]. Most of the available energy is lost here, as represented by the heat exhaust [latex]Q_2[/latex].
vi. Isobaric compression (AO). The exhaust valve remains open, and the compression from VA to zero drives out the remaining combustion products.
(a) Using (i) [latex]e=W/Q_{1}[/latex]; (ii) [latex]W=Q_{1}-Q_{2}[/latex]; and (iii) [latex]Q_{1}=nC_{v}(T_{C}-T_{B})[/latex], [latex]Q_{2}=nC_{v}(T_{D}-T_{A})[/latex], show that
(b) Use the fact that steps (ii) and (iv) are adiabatic to show that
where [latex]r=V_A/V_B[/latex]. The quantity r is called the compression ratio of the engine.
(c) In practice, r is kept less than around 7. For larger values, the gasoline-air mixture is compressed to temperatures so high that it explodes before the finely timed spark is delivered. This preignition causes engine knock and loss of power. Show that for [latex]r=6[/latex] and [latex]\gamma = 1.4[/latex] (the value for air), [latex]e=0.51[/latex], or an efficiency of 51%. Because of the many irreversible processes, an actual internal combustion engine has an efficiency much less than this ideal value. A typical efficiency for a tuned engine is about 25% to 30%.
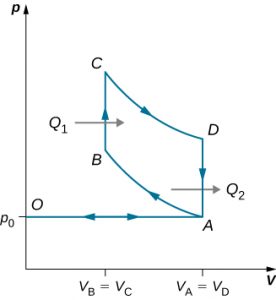
89. An ideal diesel cycle is shown below. This cycle consists of five strokes. In this case, only air is drawn into the chamber during the intake stroke OA. The air is then compressed adiabatically from state A to state B, raising its temperature high enough so that when fuel is added during the power stroke BC, it ignites. After ignition ends at C, there is a further adiabatic power stroke CD. Finally, there is an exhaust at constant volume as the pressure drops from pD to pA, followed by a further exhaust when the piston compresses the chamber volume to zero.
(a) Use [latex]W=Q_1-Q_2[/latex], [latex]Q_1=nC_p(T_C-T_B)[/latex], and [latex]Q_2=nC_v(T_D-T_A)[/latex] to show that
(b) Use the fact that [latex]A \to B[/latex] and [latex]C \to D[/latex] are adiabatic to show that
(c) Since there is no preignition (remember, the chamber does not contain any fuel during the compression), the compression ratio can be larger than that for a gasoline engine. Typically, [latex]V_A/V_B=15[/latex] and [latex]V_D/V_C=5[/latex]. For these values and [latex]\gamma = 1.4[/latex], show that [latex]\epsilon=0.56[/latex], or an efficiency of 56%. Diesel engines actually operate at an efficiency of about 30% to 35% compared with 25% to 30% for gasoline engines.
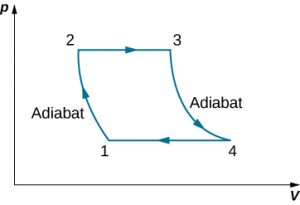
90. Consider an ideal gas Joule cycle, also called the Brayton cycle, shown below. Find the formula for efficiency of the engine using this cycle in terms of P1, P2, and [latex]\gamma[/latex].
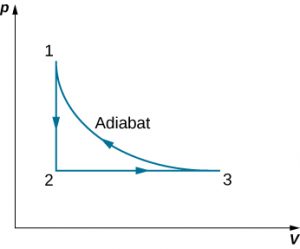
91. Derive a formula for the coefficient of performance of a refrigerator using an ideal gas as a working substance operating in the cycle shown below in terms of the properties of the three states labeled 1, 2, and 3.
92. Two moles of nitrogen gas, with [latex]\gamma = 7/5[/latex] for ideal diatomic gases, occupies a volume of [latex]10^{-2}\text{m}^{3}[/latex] in an insulated cylinder at temperature 300 K. The gas is adiabatically and reversibly compressed to a volume of 5 L. The piston of the cylinder is locked in its place, and the insulation around the cylinder is removed. The heat-conducting cylinder is then placed in a 300-K bath. Heat from the compressed gas leaves the gas, and the temperature of the gas becomes 300 K again. The gas is then slowly expanded at the fixed temperature 300 K until the volume of the gas becomes [latex]10^{-2}\text{m}^{3}[/latex], thus making a complete cycle for the gas. For the entire cycle, calculate
(a) the work done by the gas,
(b) the heat into or out of the gas,
(c) the change in the internal energy of the gas, and
(d) the change in entropy of the gas.
93. A Carnot refrigerator, working between 0°C and 30°C is used to cool a bucket of water containing [latex]10^{-2}\text{m}^{3}[/latex] of water at 30°C to 5°C in 2 hours. Find the total amount of work needed.
Media Attributions
- UP2.F4X
- UP2.F4Xa
- UP2.F4Xb
- UP2.F4Xc
- UP2.F4Xd
- UP2.F4Xe
- UP2.F4Xf

