Chapter 2 The Kinetic Theory of Gases
Chapter Review
OpenStax and Paula Herrera-Siklody
Key Terms | Key Equations | Summary | Conceptual Questions | Problems | Additional Problems | Challenge Problems
Key Terms
Avogadro’s number: [latex]N_\text{A}[/latex], the number of molecules in one mole of a substance; [latex]N_\text{A} = 6.02 \times 10^{23}[/latex] particles/mole
Boltzmann constant: [latex]k_\text{B}[/latex], a physical constant that relates energy to temperature and appears in the ideal gas law; [latex]k_\text{B} = 1.38 \times 10^{-23}\text{J/K}[/latex]
critical temperature: [latex]T_c[/latex] at which the isotherm has a point with zero slope
Dalton’s law of partial pressures: physical law that states that the total pressure of a gas is the sum of partial pressures of the component gases
degree of freedom: independent kind of motion possessing energy, such as the kinetic energy of motion in one of the three orthogonal spatial directions
equipartition theorem: theorem that the energy of a classical thermodynamic system is shared equally among its degrees of freedom
ideal gas: gas at the limit of low density and high temperature
ideal gas law: physical law that relates the pressure and volume of a gas, far from liquefaction, to the number of gas molecules or number of moles of gas and the temperature of the gas
internal energy: sum of the mechanical energies of all of the molecules in it
kinetic theory of gases: theory that derives the macroscopic properties of gases from the motion of the molecules they consist of
Maxwell-Boltzmann distribution: function that can be integrated to give the probability of finding ideal gas molecules with speeds in the range between the limits of integration
mean free path: average distance between collisions of a particle
mean free time: average time between collisions of a particle
mole: quantity of a substance whose mass (in grams) is equal to its molecular mass
most probable speed: speed near which the speeds of most molecules are found, the peak of the speed distribution function
partial pressure: pressure a gas would create if it occupied the total volume of space available
peak speed: same as “most probable speed”
pV diagram: graph of pressure vs. volume
root-mean-square (rms) speed: square root of the average of the square (of a quantity)
supercritical: condition of a fluid being at such a high temperature and pressure that the liquid phase cannot exist
universal gas constant: R, the constant that appears in the ideal gas law expressed in terms of moles, given by [latex]R=N_Ak_\text{B}[/latex]
van der Waals equation of state: equation, typically approximate, which relates the pressure and volume of a gas to the number of gas molecules or number of moles of gas and the temperature of the gas
vapor pressure: partial pressure of a vapor at which it is in equilibrium with the liquid (or solid, in the case of sublimation) phase of the same substance
Key Equations
| Ideal gas law in terms of molecules | [latex]pV = Nk_\text{B}T[/latex] |
| Ideal gas law ratios if the amount of gas is constant | [latex]\frac{p_1V_1}{T_1} = \frac{p_2V_2}{t_2}[/latex] |
| Ideal gas law in terms of moles | [latex]pV = nRT[/latex] |
| Van der Waals equation | |
| Pressure, volume, and molecular speed | [latex]pV = \frac{1}{3}Nm\bar{v^2}[/latex] |
| Root-mean-square speed | [latex]v_{\text{rms}} = \sqrt{\frac{3RT}{M}} = \sqrt{\frac{3 k_B T}{m}}[/latex] |
| Mean free path | [latex]\lambda = \frac{V}{4\sqrt{2}\pi r^2 N} = \frac{k_B T}{4\sqrt{2}\pi r^2 p}[/latex] |
| Mean free time | [latex]\tau = \frac{k_B T}{4\sqrt{2}\pi r^2 p v_{rms}}[/latex] |
| The following two equations apply only to a monatomic ideal gas: | |
| Average kinetic energy of a molecule | [latex]\bar{K} = \frac{3}{2}k_\text{B}T[/latex] |
| Internal energy | [latex]E_\text{int} = \frac{3}{2}Nk_\text{B}T[/latex] |
| Heat in terms of molar heat capacity at constant volume | [latex]Q=nC_V\Delta T[/latex] |
| Molar heat capacity at constant volume for an ideal gas with d degrees of freedom | [latex]C_V = \frac{d}{2}R[/latex] |
| Maxwell–Boltzmann speed distribution | [latex]f(v) = \frac{4}{\sqrt{\pi}} {\bigg(\frac{m}{2 k_B T}\bigg)}^{3/2} v^2 e^{-m v^2 /2 k_\text{B} T}[/latex] |
| Average velocity of a molecule | [latex]\bar{v} = \sqrt{\frac{8}{\pi}\frac{k_B T}{m}} = \sqrt{\frac{8}{\pi}\frac{RT}{M}}[/latex] |
| Peak velocity of a molecule | [latex]v_p = \sqrt{\frac{2 k_B T}{m}} = \sqrt{\frac{2RT}{M}}[/latex] |
Summary
2.1 Molecular Model of an Ideal Gas
- The ideal gas law relates the pressure and volume of a gas to the number of gas molecules and the temperature of the gas.
- A mole of any substance has a number of molecules equal to the number of atoms in a 12-g sample of carbon-12. The number of molecules in a mole is called Avogadro’s number [latex]N_\text{A}[/latex],
[latex]N_\text{A} = 6.02 \times 10^{23}\text{mol}^{-1}[/latex].
- A mole of any substance has a mass in grams numerically equal to its molecular mass in unified mass units, which can be determined from the periodic table of elements. The ideal gas law can also be written and solved in terms of the number of moles of gas:
[latex]pV = nRT,[/latex]
where n is the number of moles and R is the universal gas constant,
[latex]R = 8.31\text{J/mol}\cdot K.[/latex]
- The ideal gas law is generally valid at temperatures well above the boiling temperature.
- The van der Waals equation of state for gases is valid closer to the boiling point than the ideal gas law.
- Above the critical temperature and pressure for a given substance, the liquid phase does not exist, and the sample is “supercritical.”
2.2 Pressure, Temperature, and RMS Speed
- Kinetic theory is the atomic description of gases as well as liquids and solids. It models the properties of matter in terms of continuous random motion of molecules.
- The ideal gas law can be expressed in terms of the mass of the gas’s molecules and [latex]\bar{v^2}[/latex], the average of the molecular speed squared, instead of the temperature.
- The temperature of gases is proportional to the average translational kinetic energy of molecules. Hence, the typical speed of gas molecules [latex]v_\text{rms}[/latex] is proportional to the square root of the temperature and inversely proportional to the square root of the molecular mass.
- In a mixture of gases, each gas exerts a pressure equal to the total pressure times the fraction of the mixture that the gas makes up.
- The mean free path (the average distance between collisions) and the mean free time of gas molecules are proportional to the temperature and inversely proportional to the molar density and the molecules’ cross-sectional area.
2.3 Heat Capacity and Equipartition of Energy
- Every degree of freedom of an ideal gas contributes [latex]\frac{1}{2}k_\text{B}T[/latex] per atom or molecule to its changes in internal energy.
- Every degree of freedom contributes [latex]\frac{1}{2}R[/latex] to its molar heat capacity at constant volume [latex]C_V[/latex].
- Degrees of freedom do not contribute if the temperature is too low to excite the minimum energy of the degree of freedom as given by quantum mechanics. Therefore, at ordinary temperatures, [latex]d = 3[/latex] for monatomic gases, [latex]d = 5[/latex] for diatomic gases, and [latex]d \approx 6[/latex] for polyatomic gases.
2.4 Distribution of Molecular Speeds
- The motion of individual molecules in a gas is random in magnitude and direction. However, a gas of many molecules has a predictable distribution of molecular speeds, known as the Maxwell-Boltzmann distribution.
- The average and most probable velocities of molecules having the Maxwell-Boltzmann speed distribution, as well as the rms velocity, can be calculated from the temperature and molecular mass.
Conceptual Questions
2.1 Molecular Model of an Ideal Gas
- Two [latex]\text{H}_2[/latex] molecules can react with one [latex]\text{O}_2[/latex] molecule to produce two [latex]\text{H}_2\text{O}[/latex] molecules. How many moles of hydrogen molecules are needed to react with one mole of oxygen molecules?
- Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?
- A constant-volume gas thermometer contains a fixed amount of gas. What property of the gas is measured to indicate its temperature?
- Inflate a balloon at room temperature. Leave the inflated balloon in the refrigerator overnight. What happens to the balloon, and why?
- In the last chapter, free convection was explained as the result of buoyant forces on hot fluids. Explain the upward motion of air in flames based on the ideal gas law.
2.2 Pressure, Temperature, and RMS Speed
- How is momentum related to the pressure exerted by a gas? Explain on the molecular level, considering the behavior of molecules.
- If one kind of molecule has double the radius of another and eight times the mass, how do their mean free paths under the same conditions compare? How do their mean free times compare
- What is the average velocity of the air molecules in the room where you are right now?
- Why do the atmospheres of Jupiter, Saturn, Uranus, and Neptune, which are much more massive and farther from the Sun than Earth is, contain large amounts of hydrogen and helium?
- Statistical mechanics says that in a gas maintained at a constant temperature through thermal contact with a bigger system (a “reservoir”) at that temperature, the fluctuations in internal energy are typically a fraction [latex]1/ \sqrt{N}[/latex] of the internal energy. As a fraction of the total internal energy of a mole of gas, how big are the fluctuations in the internal energy? Are we justified in ignoring them?
- Which is more dangerous, a closet where tanks of nitrogen are stored, or one where tanks of carbon dioxide are stored?
2.3 Heat Capacity and Equipartition of Energy
- Experimentally it appears that many polyatomic molecules’ vibrational degrees of freedom can contribute to some extent to their energy at room temperature. Would you expect that fact to increase or decrease their heat capacity from the value R? Explain.
- One might think that the internal energy of diatomic gases is given by [latex]E_\text{int} = 5RT/2[/latex]. Do diatomic gases near room temperature have more or less internal energy than that? Hint: Their internal energy includes the total energy added in raising the temperature from the boiling point (very low) to room temperature.
- You mix 5 moles of [latex]\text{H}_2[/latex] at 300 K with 5 moles of He at 360 K in a perfectly insulated calorimeter. Is the final temperature higher or lower than 330 K?
2.4 Distribution of Molecular Speeds
- One cylinder contains helium gas and another contains krypton gas at the same temperature. Mark each of these statements true, false, or impossible to determine from the given information.
(a) The rms speeds of atoms in the two gases are the same.
(b) The average kinetic energies of atoms in the two gases are the same.
(c) The internal energies of 1 mole of gas in each cylinder are the same.
(d) The pressures in the two cylinders are the same. - Repeat the previous question if one gas is still helium but the other is changed to fluorine, [latex]\text{F}_2[/latex].
- An ideal gas is at a temperature of 300 K. To double the average speed of its molecules, what does the temperature need to be changed to?
Problems
2.1 Molecular Model of an Ideal Gas
- The gauge pressure in your car tires is [latex]2.50 \times 10^5\text{N/m}^2[/latex] at a temperature of [latex]35.0^\circ \text{C}[/latex] when you drive it onto a ship in Los Angeles to be sent to Alaska. What is their gauge pressure on a night in Alaska when their temperature has dropped to [latex]-40.0^\circ \text{C}[/latex] ? Assume the tires have not gained or lost any air.
- Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of [latex]20.0^\circ \text{C}[/latex].
(a) Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is [latex]60.0^\circ \text{C}[/latex] (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks.
(b) The actual final pressure for the light bulb will be less than calculated in part (a) because the glass bulb will expand. Is this effect significant? - People buying food in sealed bags at high elevations often notice that the bags are puffed up because the air inside has expanded. A bag of pretzels was packed at a pressure of 1.00 atm and a temperature of [latex]22.0^\circ \text{C}[/latex]. When opened at a summer picnic in Santa Fe, New Mexico, at a temperature of [latex]32.0^\circ \text{C}[/latex], the volume of the air in the bag is 1.38 times its original volume. What is the pressure of the air?
- How many moles are there in
(a) 0.0500 g of [latex]\text{N}_2[/latex] gas ([latex]M = 28.0\text{g/mol}[/latex])?
(b) 10.0 g of [latex]\text{CO}_2[/latex] gas ([latex]M = 44.0\text{g/mol}[/latex])?
(c) How many molecules are present in each case? - A cubic container of volume 2.00 L holds 0.500 mol of nitrogen gas at a temperature of [latex]25.0^\circ \text{C}[/latex]. What is the net force due to the nitrogen on one wall of the container? Compare that force to the sample’s weight.
- Calculate the number of moles in the 2.00-L volume of air in the lungs of the average person. Note that the air is at [latex]37.0^\circ \text{C}[/latex] (body temperature) and that the total volume in the lungs is several times the amount inhaled in a typical breath as given in Example 2.2.
- An airplane passenger has [latex]100\text{cm}^3[/latex] of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to [latex]7.50 \times 10^{4}\text{N/m}^2[/latex]?
- A company advertises that it delivers helium at a gauge pressure of [latex]1.72 \times 10^7 \text{Pa}[/latex] in a cylinder of volume 43.8 L. How many balloons can be inflated to a volume of 4.00 L with that amount of helium? Assume the pressure inside the balloons is [latex]1.01 \times 10^5 \text{Pa}[/latex] and the temperature in the cylinder and the balloons is [latex]25.0^\circ \text{C}[/latex].
- According to http://hyperphysics.phy-astr.gsu.edu/hbase/solar/venusenv.html, the atmosphere of Venus is approximately [latex]96.5\%\text{ CO}_2[/latex] and [latex]3.5\%\text{ N}_2[/latex] by volume. On the surface, where the temperature is about 750 K and the pressure is about 90 atm, what is the density of the atmosphere?
- An expensive vacuum system can achieve a pressure as low as [latex]1.00 \times 10^{-7}\text{N/m}^2[/latex] at [latex]20.0^\circ\text{C}[/latex]. How many molecules are there in a cubic centimeter at this pressure and temperature?
- The number density N/V of gas molecules at a certain location in the space above our planet is about [latex]1.00 \times 10^{11}\text{m}^{-3}[/latex], and the pressure is [latex]2.75 \times 10^{-10}\text{N/m}^2[/latex] in this space. What is the temperature there?
- A bicycle tire contains 2.00 L of gas at an absolute pressure of [latex]7.00 \times 10^5\text{N/m}^2[/latex] and a temperature of [latex]18.0^\circ\text{C}[/latex]. What will its pressure be if you let out an amount of air that has a volume of [latex]100\text{cm}^3[/latex] at atmospheric pressure? Assume tire temperature and volume remain constant.
- In a common demonstration, a bottle is heated and stoppered with a hard-boiled egg that’s a little bigger than the bottle’s neck. When the bottle is cooled, the pressure difference between inside and outside forces the egg into the bottle. Suppose the bottle has a volume of 0.500 L and the temperature inside it is raised to [latex]80.0^\circ\text{C}[/latex] while the pressure remains constant at 1.00 atm because the bottle is open.
(a) How many moles of air are inside?
(b) Now the egg is put in place, sealing the bottle. What is the gauge pressure inside after the air cools back to the ambient temperature of [latex]25^\circ\text{C}[/latex] but before the egg is forced into the bottle? - A high-pressure gas cylinder contains 50.0 L of toxic gas at a pressure of [latex]1.40 \times 10^7\text{N/m}^2[/latex] and a temperature of [latex]25.0^\circ\text{C}[/latex]. The cylinder is cooled to dry ice temperature ([latex]-78.5^\circ\text{C}[/latex]) to reduce the leak rate and pressure so that it can be safely repaired.
(a) What is the final pressure in the tank, assuming a negligible amount of gas leaks while being cooled and that there is no phase change?
(b) What is the final pressure if one-tenth of the gas escapes?
(c) To what temperature must the tank be cooled to reduce the pressure to 1.00 atm (assuming the gas does not change phase and that there is no leakage during cooling)?
(d) Does cooling the tank as in part (c) appear to be a practical solution? - Find the number of moles in 2.00 L of gas at [latex]35.0^\circ \text{C}[/latex] and under [latex]7.41 \times 10^7\text{N/m}^2[/latex] of pressure.
- Calculate the depth to which Avogadro’s number of table tennis balls would cover Earth. Each ball has a diameter of 3.75 cm. Assume the space between balls adds an extra [latex]25.0\%[/latex] to their volume and assume they are not crushed by their own weight.
- (a) What is the gauge pressure in a [latex]25.0^\circ \text{C}[/latex] car tire containing 3.60 mol of gas in a 30.0-L volume?
(b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and [latex]25.0^\circ\text{C}[/latex] ? Assume the temperature remains at [latex]25.0^\circ\text{C}[/latex] and the volume remains constant.
2.2 Pressure, Temperature, and RMS Speed
In the problems in this section, assume all gases are ideal.
- A person hits a tennis ball with a mass of 0.058 kg against a wall. The average component of the ball’s velocity perpendicular to the wall is 11 m/s, and the ball hits the wall every 2.1 s on average, rebounding with the opposite perpendicular velocity component.
(a) What is the average force exerted on the wall?
(b) If the part of the wall the person hits has an area of [latex]3.0\text{m}^2[/latex], what is the average pressure on that area? - A person is in a closed room (a racquetball court) with [latex]V = 453\text{m}^3[/latex] hitting a ball ([latex]m = 42.0\text{g}[/latex]) around at random without any pauses. The average kinetic energy of the ball is 2.30 J.
(a) What is the average value of [latex]v^2_x[/latex]? Does it matter which direction you take to be x?
(b) Applying the methods of this chapter, find the average pressure on the walls?
(c) Aside from the presence of only one “molecule” in this problem, what is the main assumption in Pressure, Temperature, and RMS Speed that does not apply here? - Five bicyclists are riding at the following speeds: 5.4 m/s, 5.7 m/s, 5.8 m/s, 6.0 m/s, and 6.5 m/s
(a) What is their average speed?
(b) What is their rms speed? - Some incandescent light bulbs are filled with argon gas. What is [latex]v_\text{rms}[/latex] for argon atoms near the filament, assuming their temperature is 2500 K?
- Typical molecular speeds ([latex]v_\text{rms}[/latex]) are large, even at low temperatures. What is [latex]v_\text{rms}[/latex] for helium atoms at 5.00 K, less than one degree above helium’s liquefaction temperature?
- (a) What is the average kinetic energy in joules of hydrogen atoms on the [latex]5500^\circ\text{C}[/latex] surface of the Sun?
(b) What is the average kinetic energy of helium atoms in a region of the solar corona where the temperature is [latex]6.00 \times 10^5\text{K}[/latex] ? - What is the ratio of the average translational kinetic energy of a nitrogen molecule at a temperature of 300 K to the gravitational potential energy of a nitrogen-molecule−Earth system at the ceiling of a 3-m-tall room with respect to the same system with the molecule at the floor?
- What is the total translational kinetic energy of the air molecules in a room of volume [latex]23\text{m}^3[/latex] if the pressure is [latex]9.5 \times 10^4\text{Pa}[/latex] (the room is at fairly high elevation) and the temperature is [latex]21^\circ\text{C}[/latex]? Is any item of data unnecessary for the solution?
- The product of the pressure and volume of a sample of hydrogen gas at [latex]0.00^\circ\text{C}[/latex] is 80.0 J.
(a) How many moles of hydrogen are present?
(b) What is the average translational kinetic energy of the hydrogen molecules?
(c) What is the value of the product of pressure and volume at [latex]200^\circ\text{C}[/latex]? - What is the gauge pressure inside a tank of [latex]4.86 \times 10^4 \text{mol}[/latex] of compressed nitrogen with a volume of 6.56m3 if the rms speed is 514 m/s?
- If the rms speed of oxygen molecules inside a refrigerator of volume [latex]22.0\text{ft}^3[/latex] is 465 m/s, what is the partial pressure of the oxygen? There are 5.71 moles of oxygen in the refrigerator, and the molar mass of oxygen is 32.0 g/mol.
- The escape velocity of any object from Earth is 11.1 km/s. At what temperature would oxygen molecules (molar mass is equal to 32.0 g/mol) have root-mean-square velocity [latex]v_\text{rms}[/latex] equal to Earth’s escape velocity of 11.1 km/s?
- The escape velocity from the Moon is much smaller than that from the Earth, only 2.38 km/s. At what temperature would hydrogen molecules (molar mass is equal to 2.016 g/mol) have a root-mean-square velocity vrms equal to the Moon’s escape velocity?
- Nuclear fusion, the energy source of the Sun, hydrogen bombs, and fusion reactors, occurs much more readily when the average kinetic energy of the atoms is high—that is, at high temperatures. Suppose you want the atoms in your fusion experiment to have average kinetic energies of [latex]6.40 \times 10^{-14}\text{J}[/latex]. What temperature is needed?
- Suppose that the typical speed ([latex]v_\text{rms}[/latex]) of carbon dioxide molecules (molar mass is 44.0 g/mol) in a flame is found to be 1350 m/s. What temperature does this indicate?
- (a) Hydrogen molecules (molar mass is equal to 2.016 g/mol) have [latex]v_\text{rms}[/latex] equal to 193 m/s. What is the temperature?
(b) Much of the gas near the Sun is atomic hydrogen (H rather than [latex]\text{H}_2[/latex]). Its temperature would have to be [latex]1.5 \times 10^7\text{K}[/latex] for the rms speed [latex]v_\text{rms}[/latex] to equal the escape velocity from the Sun. What is that velocity? - There are two important isotopes of uranium, [latex]^{235}\text{U}[/latex] and [latex]^{238}\text{U}[/latex]; these isotopes are nearly identical chemically but have different atomic masses. Only [latex]^{235}\text{U}[/latex] is very useful in nuclear reactors. Separating the isotopes is called uranium enrichment (and is often in the news as of this writing, because of concerns that some countries are enriching uranium with the goal of making nuclear weapons.) One of the techniques for enrichment, gas diffusion, is based on the different molecular speeds of uranium hexafluoride gas, [latex]\text{UF}_6[/latex].
(a) The molar masses of [latex]^{235}\text{U}[/latex] and [latex]^{238}\text{UF}_6[/latex] are 349.0 g/mol and 352.0 g/mol, respectively. What is the ratio of their typical speeds [latex]v_\text{rms}[/latex]?
(b) At what temperature would their typical speeds differ by 1.00 m/s?
(c) Do your answers in this problem imply that this technique may be difficult? - The partial pressure of carbon dioxide in the lungs is about 470 Pa when the total pressure in the lungs is 1.0 atm. What percentage of the air molecules in the lungs is carbon dioxide? Compare your result to the percentage of carbon dioxide in the atmosphere, about [latex]0.033\%[/latex].
- Dry air consists of approximately [latex]78\%\text{nitrogen}[/latex], [latex]21\%\text{oxygen}[/latex], and [latex]1\%\text{argon}[/latex] by mole, with trace amounts of other gases. A tank of compressed dry air has a volume of 1.76 cubic feet at a gauge pressure of 2200 pounds per square inch and a temperature of 293 K. How much oxygen does it contain in moles?
- (a) Using data from the previous problem, find the mass of nitrogen, oxygen, and argon in 1 mol of dry air. The molar mass of [latex]\text{N}_2[/latex] is 28.0 g/mol, that of [latex]\text{O}_2[/latex] is 32.0 g/mol, and that of argon is 39.9 g/mol.
(b) Dry air is mixed with pentane ([latex]\text{C}_5\text{H}_{12}[/latex], molar mass 72.2 g/mol), an important constituent of gasoline, in an air-fuel ratio of 15:1 by mass (roughly typical for car engines). Find the partial pressure of pentane in this mixture at an overall pressure of 1.00 atm. - (a) Given that air is [latex]21\%[/latex] oxygen, find the minimum atmospheric pressure that gives a relatively safe partial pressure of oxygen of 0.16 atm.
(b) What is the minimum pressure that gives a partial pressure of oxygen above the quickly fatal level of 0.06 atm?
(c) The air pressure at the summit of Mount Everest (8848 m) is 0.334 atm. Why have a few people climbed it without oxygen, while some who have tried, even though they had trained at high elevation, had to turn back? - (a) If the partial pressure of water vapor is 8.05 torr, what is the dew point? ([latex]760\text{torr} = 1\text{atm} = 101,325\text{Pa}[/latex])
(b) On a warm day when the air temperature is [latex]35^\circ\text{C}[/latex] and the dew point is [latex]25^\circ\text{C}[/latex], what are the partial pressure of the water in the air and the relative humidity?
2.3 Heat Capacity and Equipartition of Energy
- To give a helium atom nonzero angular momentum requires about 21.2 eV of energy (that is, 21.2 eV is the difference between the energies of the lowest-energy or ground state and the lowest-energy state with angular momentum). The electron-volt or eV is defined as [latex]1.60 \times 10^{-19}\text{J}[/latex]. Find the temperature T where this amount of energy equals [latex]k_\text{B}T/2[/latex]. Does this explain why we can ignore the rotational energy of helium for most purposes? (The results for other monatomic gases, and for diatomic gases rotating around the axis connecting the two atoms, have comparable orders of magnitude.)
- (a) How much heat must be added to raise the temperature of 1.5 mol of air from [latex]25.0^\circ\text{C}[/latex] to [latex]33.0^\circ\text{C}[/latex] at constant volume? Assume air is completely diatomic.
(b) Repeat the problem for the same number of moles of xenon, Xe. - A sealed, rigid container of 0.560 mol of an unknown ideal gas at a temperature of [latex]30.0^\circ\text{C}[/latex] is cooled to [latex]-40.0^\circ\text{C}[/latex]. In the process, 980 J of heat are removed from the gas. Is the gas monatomic, diatomic, or polyatomic?
- A sample of neon gas (Ne, molar mass [latex]M = 20.2\text{g/mol}[/latex]) at a temperature of [latex]13.0^\circ\text{C}[/latex] is put into a steel container of mass 47.2 g that’s at a temperature of [latex]-40.0^\circ\text{C}[/latex]. The final temperature is [latex]-28.0^\circ\text{C}[/latex]. (No heat is exchanged with the surroundings, and you can neglect any change in the volume of the container.) What is the mass of the sample of neon?
- A steel container of mass 135 g contains 24.0 g of ammonia, [latex]\text{NH}_3[/latex], which has a molar mass of 17.0 g/mol. The container and gas are in equilibrium at [latex]12.0^\circ\text{C}[/latex]. How much heat has to be removed to reach a temperature of [latex]-20.0^\circ\text{C}[/latex] ? Ignore the change in volume of the steel.
- A sealed room has a volume of [latex]24\text{m}^3[/latex]. It’s filled with air, which may be assumed to be diatomic, at a temperature of [latex]24^\circ\text{C}[/latex] and a pressure of [latex]9.83 \times 10^4\text{Pa}[/latex]. A 1.00-kg block of ice at its melting point is placed in the room. Assume the walls of the room transfer no heat. What is the equilibrium temperature?
- Heliox, a mixture of helium and oxygen, is sometimes given to hospital patients who have trouble breathing, because the low mass of helium makes it easier to breathe than air. Suppose helium at [latex]25^\circ\text{C}[/latex] is mixed with oxygen at [latex]35^\circ\text{C}[/latex] to make a mixture that is [latex]70\%[/latex] helium by mole. What is the final temperature? Ignore any heat flow to or from the surroundings, and assume the final volume is the sum of the initial volumes.
- Professional divers sometimes use heliox, consisting of [latex]79\%[/latex] helium and [latex]21\%[/latex] oxygen by mole. Suppose a perfectly rigid scuba tank with a volume of 11 L contains heliox at an absolute pressure of [latex]2.1 \times 10^7\text{Pa}[/latex] at a temperature of [latex]31^\circ\text{C}[/latex].
(a) How many moles of helium and how many moles of oxygen are in the tank?
(b) The diver goes down to a point where the sea temperature is [latex]27^\circ\text{C}[/latex] while using a negligible amount of the mixture. As the gas in the tank reaches this new temperature, how much heat is removed from it? - In car racing, one advantage of mixing liquid nitrous oxide ([latex]\text{N}_2\text{O}[/latex]) with air is that the boiling of the “nitrous” absorbs latent heat of vaporization and thus cools the air and ultimately the fuel-air mixture, allowing more fuel-air mixture to go into each cylinder. As a very rough look at this process, suppose 1.0 mol of nitrous oxide gas at its boiling point, [latex]-88^\circ\text{C}[/latex], is mixed with 4.0 mol of air (assumed diatomic) at [latex]30^\circ\text{C}[/latex]. What is the final temperature of the mixture? Use the measured heat capacity of [latex]\text{N}_2\text{O}[/latex] at [latex]25^\circ\text{C}[/latex], which is [latex]30.4\text{J/mol}^\circ\text{C}[/latex]. (The primary advantage of nitrous oxide is that it consists of 1/3 oxygen, which is more than air contains, so it supplies more oxygen to burn the fuel. Another advantage is that its decomposition into nitrogen and oxygen releases energy in the cylinder.)
2.4 Distribution of Molecular Speeds
- In a sample of hydrogen sulfide ([latex]M = 34.1\text{g/mol}[/latex]) at a temperature of [latex]3.00 \times 10^{2}\text{K}[/latex], estimate the ratio of the number of molecules that have speeds very close to [latex]v_\text{rms}[/latex] to the number that have speeds very close to 2[latex]v_\text{rms}[/latex].
- Using the approximation [latex]\int_{v_1}^{v_1 + \Delta v} f(v)dv \approx f( v_1 )\Delta v[/latex] for small [latex]\Delta v[/latex], estimate the fraction of nitrogen molecules at a temperature of [latex]3.00 \times 10^2\text{K}[/latex] that have speeds between 290 m/s and 291 m/s.
- Using the method of the preceding problem, estimate the fraction of nitric oxide (NO) molecules at a temperature of 250 K that have energies between [latex]3.45 \times 10^{-21}\text{J}[/latex] and [latex]3.50 \times 10^{-21}\text{J}[/latex].
- By counting squares in the following figure, estimate the fraction of argon atoms at [latex]T = 300\text{K}[/latex] that have speeds between 600 m/s and 800 m/s. The curve is correctly normalized. The value of a square is its length as measured on the x-axis times its height as measured on the y-axis, with the units given on those axes.
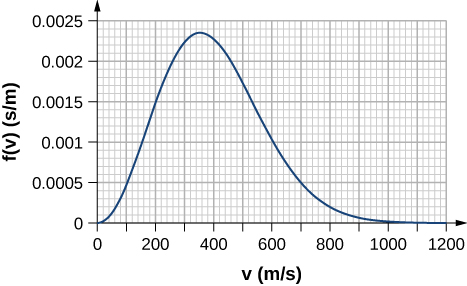
- Using a numerical integration method such as Simpson’s rule, find the fraction of molecules in a sample of oxygen gas at a temperature of 250 K that have speeds between 100 m/s and 150 m/s. The molar mass of oxygen ([latex]\text{O}_2[/latex]) is 32.0 g/mol. A precision to two significant digits is enough.
- Find (a) the most probable speed, (b) the average speed, and (c) the rms speed for nitrogen molecules at 295 K.
- Repeat the preceding problem for nitrogen molecules at 2950 K.
- At what temperature is the average speed of carbon dioxide molecules ([latex]M = 44.0\text{g/mol}[/latex]) 510 m/s?
- The most probable speed for molecules of a gas at 296 K is 263 m/s. What is the molar mass of the gas? (You might like to figure out what the gas is likely to be.)
- (a) At what temperature do oxygen molecules have the same average speed as helium atoms ([latex]M = 4.00\text{g/mol}[/latex]) have at 300 K?
(b) What is the answer to the same question about most probable speeds?
(c) What is the answer to the same question about rms speeds?
Additional Problems
- In the deep space between galaxies, the density of molecules (which are mostly single atoms) can be as low as [latex]10^6\text{atoms/m}^3[/latex], and the temperature is a frigid 2.7 K.
(a) What is the pressure?
(b) What volume (in [latex]\text{m}^3[/latex]) is occupied by 1 mol of gas?
(c) If this volume is a cube, what is the length of its sides in kilometers? - (a) Find the density in SI units of air at a pressure of 1.00 atm and a temperature of [latex]20^\circ\text{C}[/latex], assuming that air is [latex]78\%\text{ N}_2[/latex], [latex]21\%\text{O}_2[/latex], and [latex]1\%\text{Ar}[/latex],
(b) Find the density of the atmosphere on Venus, assuming that it’s [latex]96\%\text{CO}_2[/latex] and [latex]4\%\text{N}_2[/latex], with a temperature of 737 K and a pressure of 92.0 atm. - The air inside a hot-air balloon has a temperature of 370 K and a pressure of 101.3 kPa, the same as that of the air outside. Using the composition of air as [latex]78\%\text{N}_2[/latex], [latex]21\%\text{O}_2[/latex], and [latex]1\%\text{Ar}[/latex], find the density of the air inside the balloon.
- When an air bubble rises from the bottom to the top of a freshwater lake, its volume increases by [latex]80\%[/latex]. If the temperatures at the bottom and the top of the lake are 4.0 and 10 [latex]^\circ\text{C}[/latex], respectively, how deep is the lake?
- (a) Use the ideal gas equation to estimate the temperature at which 1.00 kg of steam (molar mass [latex]M = 18.0\text{g/mol}[/latex]) at a pressure of [latex]1.50 \times 10^6\text{Pa}[/latex] occupies a volume of [latex]0.220\text{m}^3[/latex].
(b) The van der Waals constants for water are [latex]a = 0.5537\text{Pa}\cdot\text{m}^6\text{/mol}^2[/latex] and [latex]b = 3.049 \times 10^{-5}\text{m}^3\text{/mol}[/latex]. Use the Van der Waals equation of state to estimate the temperature under the same conditions.
(c) The actual temperature is 779 K. Which estimate is better? - One process for decaffeinating coffee uses carbon dioxide ([latex]M = 44.0\text{g/mol}[/latex]) at a molar density of about [latex]14,600\text{mol/m}^3[/latex] and a temperature of about [latex]60^\circ\text{C}[/latex].
(a) Is [latex]\text{CO}_2[/latex] a solid, liquid, gas, or supercritical fluid under those conditions?
(b) The van der Waals constants for carbon dioxide are [latex]a = 0.3658\text{Pa}\cdot\text{m}^6\text{/mol}^2[/latex] and [latex]b = 4.286 \times 10^{-5}\text{m}^{3}\text{/mol}[/latex]. Using the van der Waals equation, estimate the pressure of [latex]\text{CO}_2[/latex] at that temperature and density. - On a winter day when the air temperature is [latex]0^\circ\text{C}[/latex], the relative humidity is [latex]50\%[/latex]. Outside air comes inside and is heated to a room temperature of [latex]20^\circ\text{C}[/latex]. What is the relative humidity of the air inside the room. (Does this problem show why inside air is so dry in winter?)
- On a warm day when the air temperature is [latex]30^\circ\text{C}[/latex], a metal can is slowly cooled by adding bits of ice to liquid water in it. Condensation first appears when the can reaches [latex]15^\circ\text{C}[/latex]. What is the relative humidity of the air?
- (a) People often think of humid air as “heavy.” Compare the densities of air with [latex]0\%[/latex] relative humidity and [latex]100\%[/latex] relative humidity when both are at 1 atm and [latex]30^\circ\text{C}[/latex]. Assume that the dry air is an ideal gas composed of molecules with a molar mass of 29.0 g/mol and the moist air is the same gas mixed with water vapor.
(b) As discussed in the chapter on the applications of Newton’s laws, the air resistance felt by projectiles such as baseballs and golf balls is approximately [latex]F_\text{D} = C\rho Av^2/2[/latex], where [latex]\rho[/latex] is the mass density of the air, A is the cross-sectional area of the projectile, and C is the projectile’s drag coefficient. For a fixed air pressure, describe qualitatively how the range of a projectile changes with the relative humidity.
(c) When a thunderstorm is coming, usually the humidity is high and the air pressure is low. Do those conditions give an advantage or disadvantage to home-run hitters? - The mean free path for helium at a certain temperature and pressure is [latex]2.10 \times 10^{-7}\text{m}[/latex]. The radius of a helium atom can be taken as [latex]1.10 \times 10^{-11}\text{m}[/latex]. What is the measure of the density of helium under those conditions (a) in molecules per cubic meter and (b) in moles per cubic meter?
- The mean free path for methane at a temperature of 269 K and a pressure of [latex]1.11 \times 10^5\text{Pa}[/latex] is [latex]4.81 \times 10^{-8}\text{m}[/latex]. Find the effective radius r of the methane molecule.
- In the chapter on fluid mechanics, Bernoulli’s equation for the flow of incompressible fluids was explained in terms of changes affecting a small volume dV of fluid. Such volumes are a fundamental idea in the study of the flow of compressible fluids such as gases as well. For the equations of hydrodynamics to apply, the mean free path must be much less than the linear size of such a volume, [latex]a \approx dV^{1/3}[/latex]. For air in the stratosphere at a temperature of 220 K and a pressure of 5.8 kPa, how big should a be for it to be 100 times the mean free path? Take the effective radius of air molecules to be [latex]1.88 \times 10^{-11}\text{m}[/latex], which is roughly correct for [latex]\text{N}_2[/latex].
- Find the total number of collisions between molecules in 1.00 s in 1.00 L of nitrogen gas at standard temperature and pressure ([latex]0^\circ\text{C}[/latex], 1.00 atm). Use [latex]1.88 \times 10^{-10}\text{m}[/latex] as the effective radius of a nitrogen molecule. (The number of collisions per second is the reciprocal of the collision time.) Keep in mind that each collision involves two molecules, so if one molecule collides once in a certain period of time, the collision of the molecule it hit cannot be counted.
- (a) Estimate the specific heat capacity of sodium from the Law of Dulong and Petit. The molar mass of sodium is 23.0 g/mol.
(b) What is the percent error of your estimate from the known value, [latex]1230\text{J/kg}\cdot^\circ\text{C}[/latex]? - A sealed, perfectly insulated container contains 0.630 mol of air at [latex]20.0^\circ\text{C}[/latex] and an iron stirring bar of mass 40.0 g. The stirring bar is magnetically driven to a kinetic energy of 50.0 J and allowed to slow down by air resistance. What is the equilibrium temperature?
- Find the ratio [latex]f(v_p)/f(v_{rms})[/latex] for hydrogen gas ([latex]M = 2.02\text{g/mol}[/latex]) at a temperature of 77.0 K.
- Unreasonable results.
(a) Find the temperature of 0.360 kg of water, modeled as an ideal gas, at a pressure of [latex]1.01 \times 10^5\text{Pa}[/latex] if it has a volume of [latex]0.615\text{m}^3[/latex].
(b) What is unreasonable about this answer? How could you get a better answer? - Unreasonable results.
(a) Find the average speed of hydrogen sulfide, [latex]\text{H}_2\text{S}[/latex], molecules at a temperature of 250 K. Its molar mass is 31.4 g/mol
(b) The result isn’t very unreasonable, but why is it less reliable than those for, say, neon or nitrogen?
Challenge Problems
- An airtight dispenser for drinking water is [latex]25\text{cm} \times 10\text{cm}[/latex] in horizontal dimensions and 20 cm tall. It has a tap of negligible volume that opens at the level of the bottom of the dispenser. Initially, it contains water to a level 3.0 cm from the top and air at the ambient pressure, 1.00 atm, from there to the top. When the tap is opened, water will flow out until the gauge pressure at the bottom of the dispenser, and thus at the opening of the tap, is 0. What volume of water flows out? Assume the temperature is constant, the dispenser is perfectly rigid, and the water has a constant density of [latex]1000\text{kg/m}^3[/latex].
- Eight bumper cars, each with a mass of 322 kg, are running in a room 21.0 m long and 13.0 m wide. They have no drivers, so they just bounce around on their own. The rms speed of the cars is 2.50 m/s. Repeating the arguments of Pressure, Temperature, and RMS Speed, find the average force per unit length (analogous to pressure) that the cars exert on the walls.
- Verify that [latex]v_p = \sqrt{\frac{2 k_B T}{m}}[/latex].
- Verify the normalization equation [latex]{\displaystyle \int_{0}^{\infty}} f(v)dv = 1[/latex]. In doing the integral, first make the substitution [latex]u = \sqrt{\frac{m}{2 k_\text{B} T}}v = \frac{v}{v_p}[/latex]. This “scaling” transformation gives you all features of the answer except for the integral, which is a dimensionless numerical factor. You’ll need the formula [latex]{\displaystyle \int_{0}^{\infty}} x^2 e^{-x^2}dx = \frac{\sqrt{\pi}}{4}[/latex] to find the numerical factor and verify the normalization.
- Verify that [latex]\bar{v} = \sqrt{\frac{8}{\pi}\frac{k_\text{B} T}{m}}[/latex]. Make the same scaling transformation as in the preceding problem.
- Verify that [latex]v_{rms} = \sqrt{\bar{v^2}} = \sqrt{\frac{3 k_\text{B} T}{m}}[/latex].

