Chapter 29 The Big Bang
29.1 The Age of the Universe
Learning Objectives
By the end of this section, you will be able to:
- Describe how we estimate the age of the universe
- Explain how changes in the rate of expansion over time affect estimates of the age of the universe
- Describe the evidence that dark energy exists and that the rate of expansion is currently accelerating
- Describe some independent evidence for the age of the universe that is consistent with the age estimate based on the rate of expansion
To explore the history of the universe, we will follow the same path that astronomers followed historically—beginning with studies of the nearby universe and then probing ever-more-distant objects and looking further back in time.
The realization that the universe changes with time came in the 1920s and 1930s when measurements of the redshifts of a large sample of galaxies became available. With hindsight, it is surprising that scientists were so shocked to discover that the universe is expanding. In fact, our theories of gravity demand that the universe must be either expanding or contracting. To show what we mean, let’s begin with a universe of finite size—say a giant ball of a thousand galaxies. All these galaxies attract each other because of their gravity. If they were initially stationary, they would inevitably begin to move closer together and eventually collide. They could avoid this collapse only if for some reason they happened to be moving away from each other at high speeds. In just the same way, only if a rocket is launched at high enough speed can it avoid falling back to Earth.
The problem of what happens in an infinite universe is harder to solve, but Einstein (and others) used his theory of general relativity (which we described in Black Holes and Curved Spacetime) to show that even infinite universes cannot be static. Since astronomers at that time did not yet know the universe was expanding (and Einstein himself was philosophically unwilling to accept a universe in motion), he changed his equations by introducing an arbitrary new term (we might call it a fudge factor) called the cosmological constant. This constant represented a hypothetical force of repulsion that could balance gravitational attraction on the largest scales and permit galaxies to remain at fixed distances from one another. That way, the universe could remain still.
About a decade later, Hubble, and his coworkers reported that the universe is expanding, so that no mysterious balancing force is needed. (We discussed this in the chapter on Galaxies.) Einstein is reported to have said that the introduction of the cosmological constant was “the biggest blunder of my life.” As we shall see later in this chapter, however, relatively recent observations indicate that the expansion is accelerating. Observations are now being carried out to determine whether this acceleration is consistent with a cosmological constant. In a way, it may turn out that Einstein was right after all.
The Hubble Time
If we had a movie of the expanding universe and ran the film backward, what would we see? The galaxies, instead of moving apart, would move together in our movie—getting closer and closer all the time. Eventually, we would find that all the matter we can see today was once concentrated in an infinitesimally small volume. Astronomers identify this time with the beginning of the universe. The explosion of that concentrated universe at the beginning of time is called the Big Bang (not a bad term, since you can’t have a bigger bang than one that creates the entire universe). But when did this bang occur?
We can make a reasonable estimate of the time since the universal expansion began. To see how astronomers do this, let’s begin with an analogy. Suppose your astronomy class decides to have a party (a kind of “Big Bang”) at someone’s home to celebrate the end of the semester. Unfortunately, everyone is celebrating with so much enthusiasm that the neighbors call the police, who arrive and send everyone away at the same moment. You get home at 2 a.m., still somewhat upset about the way the party ended, and realize you forgot to look at your watch to see what time the police got there. But you use a map to measure that the distance between the party and your house is 40 kilometers. And you also remember that you drove the whole trip at a steady speed of 80 kilometers/hour (since you were worried about the police cars following you). Therefore, the trip must have taken:
![]()
So the party must have broken up at 1:30 a.m.
No humans were around to look at their watches when the universe began, but we can use the same technique to estimate when the galaxies began moving away from each other. (Remember that, in reality, it is space that is expanding, not the galaxies that are moving through static space.) If we can measure how far apart the galaxies are now, and how fast they are moving, we can figure out how long a trip it’s been.
Let’s call the age of the universe measured in this way T0. Let’s first do a simple case by assuming that the expansion has been at a constant rate ever since the expansion of the universe began. In this case, the time it has taken a galaxy to move a distance, d, away from the Milky Way (remember that at the beginning the galaxies were all together in a very tiny volume) is (as in our example)
![]()
where v is the velocity of the galaxy. If we can measure the speed with which galaxies are moving away, and also the distances between them, we can establish how long ago the expansion began.
Making such measurements should sound very familiar. This is just what Hubble and many astronomers after him needed to do in order to establish the Hubble law and the Hubble constant. We learned in Galaxies that a galaxy’s distance and its velocity in the expanding universe are related by
![]()
where H is the Hubble constant. Combining these two expressions gives us
![]()
We see, then, that the work of calculating this time was already done for us when astronomers measured the Hubble constant. The age of the universe estimated in this way turns out to be just the reciprocal of the Hubble constant (that is, 1/H). This age estimate is sometimes called the Hubble time. For a Hubble constant of 20 kilometers/second per million light-years, the Hubble time is about 15 billion years. The unit used by astronomers for the Hubble constant is kilometers/second per million parsecs. In these units, the Hubble constant is equal to about 70 kilometers/second per million parsecs, again with an uncertainty of about 5%.
To make numbers easier to remember, we have done some rounding here. Estimates for the Hubble constant are actually closer to 21 or 22 kilometers/second per million light-years, which would make the age closer to 14 billion years. But there is still about a 5% uncertainty in the Hubble constant, which means the age of the universe estimated in this way is also uncertain by about 5%.
To put these uncertainties in perspective, however, you should know that 50 years ago, the uncertainty was a factor of 2. Remarkable progress toward pinning down the Hubble constant has been made in the last couple of decades.
The Role of Deceleration
The Hubble time is the right age for the universe only if the expansion rate has been constant throughout the time since the expansion of the universe began. Continuing with our end-of-the-semester-party analogy, this is equivalent to assuming that you traveled home from the party at a constant rate, when in fact this may not have been the case. At first, mad about having to leave, you may have driven fast, but then as you calmed down—and thought about police cars on the highway—you may have begun to slow down until you were driving at a more socially acceptable speed (such as 80 kilometers/hour). In this case, given that you were driving faster at the beginning, the trip home would have taken less than a half-hour.
In the same way, in calculating the Hubble time, we have assumed that H has been constant throughout all of time. It turns out that this is not a good assumption. Earlier in their thinking about this, astronomers expected that the rate of expansion should be slowing down. We know that matter creates gravity, whereby all objects pull on all other objects. The mutual attraction between galaxies was expected to slow the expansion as time passed. This means that, if gravity were the only force acting (a big if, as we shall see in the next section), then the rate of expansion must have been faster in the past than it is today. In this case, we would say the universe has been decelerating since the beginning.
How much it has decelerated depends on the importance of gravity in slowing the expansion. If the universe were nearly empty, the role of gravity would be minor. Then the deceleration would be close to zero, and the universe would have been expanding at a constant rate. But in a universe with any significant density of matter, the pull of gravity means that the rate of expansion should be slower now than it used to be. If we use the current rate of expansion to estimate how long it took the galaxies to reach their current separations, we will overestimate the age of the universe—just as we may have overestimated the time it took for you to get home from the party.
A Universal Acceleration
Astronomers spent several decades looking for evidence that the expansion was decelerating, but they were not successful. What they needed were 1) larger telescopes so that they could measure the redshifts of more distant galaxies and 2) a very luminous standard bulb (or standard candle), that is, some astronomical object with known luminosity that produces an enormous amount of energy and can be observed at distances of a billion light-years or more.
Recall that we discussed standard bulbs in the chapter on Galaxies. If we compare how luminous a standard bulb is supposed to be and how dim it actually looks in our telescopes, the difference allows us to calculate its distance. The redshift of the galaxy such a bulb is in can tell us how fast it is moving in the universe. So we can measure its distance and motion independently.
These two requirements were finally met in the 1990s. Astronomers showed that supernovae of type Ia (see The Death of Stars), with some corrections based on the shapes of their light curves, are standard bulbs. This type of supernova occurs when a white dwarf accretes enough material from a companion star to exceed the Chandrasekhar limit and then collapses and explodes. At the time of maximum brightness, these dramatic supernovae can briefly outshine the galaxies that host them, and hence, they can be observed at very large distances. Large 8- to 10-meter telescopes can be used to obtain the spectra needed to measure the redshifts of the host galaxies ([link]).
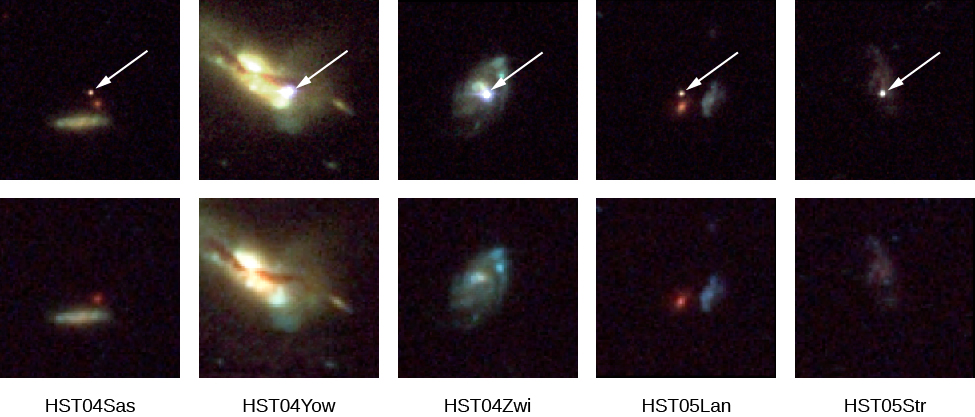
The result of painstaking, careful study of these supernovae in a range of galaxies, carried out by two groups of researchers, was published in 1998. It was shocking—and so revolutionary that their discovery received the 2011 Nobel Prize in Physics. What the researchers found was that these type Ia supernovae in distant galaxies were fainter than expected from Hubble’s law, given the measured redshifts of their host galaxies. In other words, distances estimated from the supernovae used as standard bulbs disagreed with the distances measured from the redshifts.
If the universe were decelerating, we would expect the far-away supernovae to be brighter than expected. The slowing down would have kept them closer to us. Instead, they were fainter, which at first seemed to make no sense.
Before accepting this shocking development, astronomers first explored the possibility that the supernovae might not really be as useful as standard bulbs as they thought. Perhaps the supernovae appeared too faint because dust along our line of sight to them absorbed some of their light. Or perhaps the supernovae at large distances were for some reason intrinsically less luminous than nearby supernovae of type Ia.
A host of more detailed observations ruled out these possibilities. Scientists then had to consider the alternative that the distance estimated from the redshift was incorrect. Distances derived from redshifts assume that the Hubble constant has been truly constant for all time. We saw that one way it might not be constant is that the expansion is slowing down. But suppose neither assumption is right (steady speed or slowing down.)
Suppose, instead, that the universe is accelerating. If the universe is expanding faster now than it was billions of years ago, our motion away from the distant supernovae has sped up since the explosion occurred, sweeping us farther away from them. The light of the explosion has to travel a greater distance to reach us than if the expansion rate were constant. The farther the light travels, the fainter it appears. This conclusion would explain the supernova observations in a natural way, and this has now been substantiated by many additional observations over the last couple of decades. It really seems that the expansion of the universe is accelerating, a notion so unexpected that astronomers at first resisted considering it.
How can the expansion of the universe be speeding up? If you want to accelerate your car, you must supply energy by stepping on the gas. Similarly, energy must be supplied to accelerate the expansion of the universe. The discovery of the acceleration was shocking because scientists still have no idea what the source of the energy is. Scientists call whatever it is dark energy, which is a clear sign of how little we understand it.
Note that this new component of the universe is not the dark matter we talked about in earlier chapters. Dark energy is something else that we have also not yet detected in our laboratories on Earth.
What is dark energy? One possibility is that it is the cosmological constant, which is an energy associated with the vacuum of “empty” space itself. Quantum mechanics (the intriguing theory of how things behave at the atomic and subatomic levels) tells us that the source of this vacuum energy might be tiny elementary particles that flicker in and out of existence everywhere throughout the universe. Various attempts have been made to calculate how big the effects of this vacuum energy should be, but so far these attempts have been unsuccessful. In fact, the order of magnitude of theoretical estimates of the vacuum energy based on the quantum mechanics of matter and the value required to account for the acceleration of the expansion of the universe differ by an incredible factor of at least 10120 (that is a 1 followed by 120 zeros)! Various other theories have been suggested, but the bottom line is that, although there is compelling evidence that dark energy exists, we do not yet know the source of that energy.
Whatever the dark energy turns out to be, we should note that the discovery that the rate of expansion has not been constant since the beginning of the universe complicates the calculation of the age of the universe. Interestingly, the acceleration seems not to have started with the Big Bang. During the first several billion years after the Big Bang, when galaxies were close together, gravity was strong enough to slow the expansion. As galaxies moved farther apart, the effect of gravity weakened. Several billion years after the Big Bang, dark energy took over, and the expansion began to accelerate ([link]).
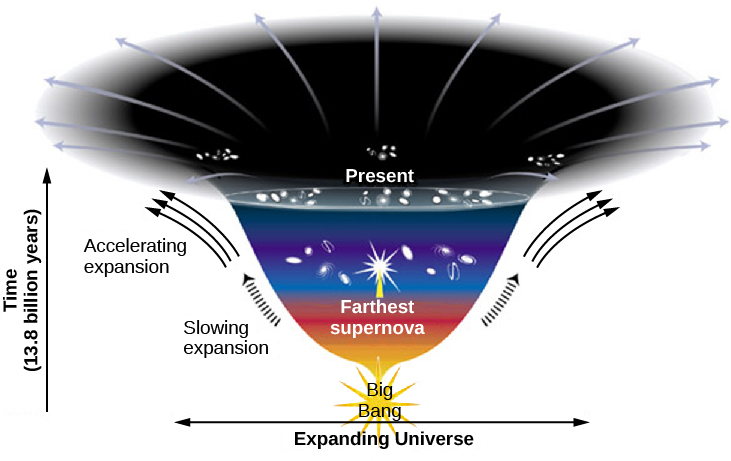
Deceleration works to make the age of the universe estimated by the simple relation T0 = 1/H seem older than it really is, whereas acceleration works to make it seem younger. By happy coincidence, our best estimates of how much deceleration and acceleration occurred lead to an answer for the age very close to T0 = 1/H . The best current estimate is that the universe is 13.8 billion years old with an uncertainty of only about 100 million years.
Throughout this chapter, we have referred to the Hubble constant. We now know that the Hubble constant does change with time. It is, however, constant everywhere in the universe at any given time. When we say the Hubble constant is about 70 kilometers/second/million parsecs, we mean that this is the value of the Hubble constant at the current time.
Comparing Ages
We now have one estimate for the age of the universe from its expansion. Is this estimate consistent with other observations? For example, are the oldest stars or other astronomical objects younger than 13.8 billion years? After all, the universe has to be at least as old as the oldest objects in it.
In our Galaxy and others, the oldest stars are found in the globular clusters ([link]), which can be dated using the models of stellar evolution described in the chapter Stars from Adolescence to Old Age.

The accuracy of the age estimates of the globular clusters has improved markedly in recent years for two reasons. First, models of interiors of globular cluster stars have been improved, mainly through better information about how atoms absorb radiation as they make their way from the center of a star out into space. Second, observations from satellites have improved the accuracy of our measurements of the distances to these clusters. The conclusion is that the oldest stars formed about 12–13 billion years ago.
This age estimate has recently been confirmed by the study of the spectrum of uranium in the stars. The isotope uranium-238 is radioactive and decays (changes into another element) over time. (Uranium-238 gets its designation because it has 92 protons and 146 neutrons.) We know (from how stars and supernovae make elements) how much uranium-238 is generally made compared to other elements. Suppose we measure the amount of uranium relative to nonradioactive elements in a very old star and in our own Sun, and compare the abundances. With those pieces of information, we can estimate how much longer the uranium has been decaying in the very old star because we know from our own Sun how much uranium decays in 4.5 billion years.
The line of uranium is very weak and hard to make out even in the Sun, but it has now been measured in one extremely old star using the European Very Large Telescope ([link]). Comparing the abundance with that in the solar system, whose age we know, astronomers estimate the star is 12.5 billion years old, with an uncertainty of about 3 billion years. While the uncertainty is large, this work is important confirmation of the ages estimated by studies of the globular cluster stars. Note that the uranium age estimate is completely independent; it does not depend on either the measurement of distances or on models of the interiors of stars.

As we shall see later in this chapter, the globular cluster stars probably did not form until the expansion of the universe had been underway for at least a few hundred million years. Accordingly, their ages are consistent with the 13.8 billion-year age estimated from the expansion rate.
Key Concepts and Summary
Cosmology is the study of the organization and evolution of the universe. The universe is expanding, and this is one of the key observational starting points for modern cosmological theories. Modern observations show that the rate of expansion has not been constant throughout the life of the universe. Initially, when galaxies were close together, the effects of gravity were stronger than the effects of dark energy, and the expansion rate gradually slowed. As galaxies moved farther apart, the influence of gravity on the expansion rate weakened. Measurements of distant supernovae show that when the universe was about half its current age, dark energy began to dominate the rate of expansion and caused it to speed up. In order to estimate the age of the universe, we must allow for changes in the rate of expansion. After allowing for these effects, astronomers estimate that all of the matter within the observable universe was concentrated in an extremely small volume 13.8 billion years ago, a time we call the Big Bang.
Glossary
- Big Bang
- the theory of cosmology in which the expansion of the universe began with a primeval explosion (of space, time, matter, and energy)
- cosmological constant
- the term in the equations of general relativity that represents a repulsive force in the universe
- cosmology
- the study of the organization and evolution of the universe
- dark energy
- the energy that is causing the expansion of the universe to accelerate; its existence is inferred from observations of distant supernovae

